题目链接

牛客网

题目描述

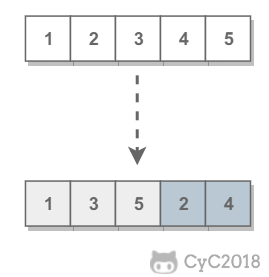
需要保证奇数和奇数，偶数和偶数之间的相对位置不变，这和书本不太一样。例如对于 [1,2,3,4,5]，调整后得到 [1,3,5,2,4]，而不能是 {5,1,3,4,2} 这种相对位置改变的结果。

解题思路

方法一：

创建一个新数组，时间复杂度 O(N)，空间复杂度 O(N)。

class Solution {
public:
    void reOrderArray(vector<int> &array) {
        int N = array.size();
        if(N==0||N==1)
            return;
        vector<int> nums(array.begin(),array.end());
        int s = 0,j=0; // s记录奇数的个数
        for(int i=0;i<N;i++){
            if(!isEven(array[i]))
                s++;
        }
        for(int i=0;i<N;i++){
            if(isEven(nums[i])){
                array[s++] = nums[i];
            }else{
                array[j++] = nums[i];
            }
        }
    }
    // 判断奇偶数
    bool isEven(int n){
       return n%2==0;
    }
};

方法二：双指针（如果不考虑相对位置）

LeetCode

• 定义头指针 left ，尾指针 right .
• left 一直往右移，直到它指向的值为偶数
• right 一直往左移， 直到它指向的值为奇数
• 交换 nums[left] 和 nums[right]
• 重复上述操作，直到 left == right

class Solution {
public:
    vector<int> exchange(vector<int>& nums) {
        int N = nums.size();
        if(N==0||N==1)
            return nums;
        int left=0,right = N-1;
        while(left<right){
            if(!isEven(nums[left])){
                left++;
                continue;
            }
            if(isEven(nums[right])){
                right--;
                continue;
            }
            swap(nums[left],nums[right]);
        }
        return nums;

    }
    bool isEven(int n){
        return n%2==0;
    }
};

• 时间复杂度 O(N/2)
• 空间复杂度 O(1)