题目链接

LeetCode

题目描述

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。

k 是一个正整数，它的值小于或等于链表的长度。

如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

进阶：

你可以设计一个只使用常数额外空间的算法来解决此问题吗？
你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

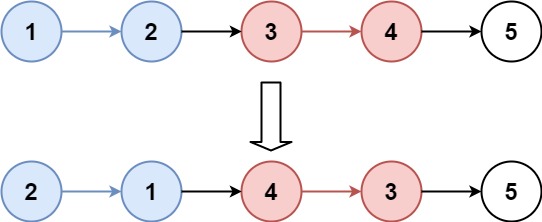
25. K 个一组翻转链表* - 图1

输入： head = [1,2,3,4,5], k = 2
输出： [2,1,4,3,5]

示例 2：

25. K 个一组翻转链表* - 图2

输入： head = [1,2,3,4,5], k = 3
输出： [3,2,1,4,5]

示例 3：

输入： head = [1,2,3,4,5], k = 1
输出： [1,2,3,4,5]

示例 4：

输入： head = [1], k = 1
输出： [1]

提示：

列表中节点的数量在范围 sz 内
1 <= sz <= 5000
0 <= Node.val <= 1000
1 <= k <= sz
解题思路
方法一：
思路与算法

本题的目标非常清晰易懂，不涉及复杂的算法，但是实现过程中需要考虑的细节比较多，容易写出冗长的代码。主要考查面试者设计的能力。

我们需要把链表节点按照 k 个一组分组，所以可以使用一个指针 head 依次指向每组的头节点。这个指针每次向前移动 k 步，直至链表结尾。对于每个分组，我们先判断它的长度是否大于等于 k。若是，我们就翻转这部分链表，否则不需要翻转。

接下来的问题就是如何翻转一个分组内的子链表。翻转一个链表并不难，过程可以参考「206. 反转链表」。但是对于一个子链表，除了翻转其本身之外，还需要将子链表的头部与上一个子链表连接，以及子链表的尾部与下一个子链表连接。如下图所示：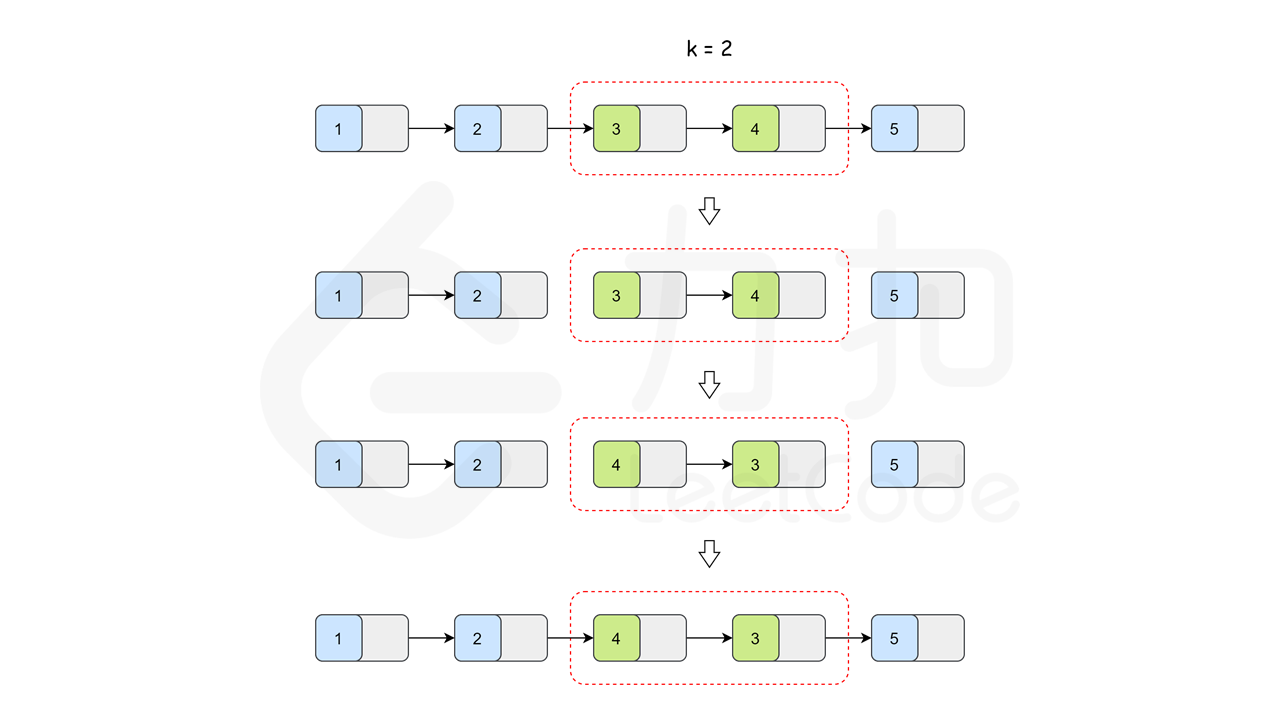
25. K 个一组翻转链表* - 图3
因此，在翻转子链表的时候，我们不仅需要子链表头节点 head，还需要有 head 的上一个节点 pre，以便翻转完后把子链表再接回 pre。

但是对于第一个子链表，它的头节点 head 前面是没有节点 pre 的。太麻烦了！难道只能特判了吗？答案是否定的。没有条件，我们就创造条件；没有节点，我们就创建一个节点。我们新建一个节点，把它接到链表的头部，让它作为 pre 的初始值，这样 head 前面就有了一个节点，我们就可以避开链表头部的边界条件。这么做还有一个好处，下面我们会看到。

反复移动指针 head 与 pre，对 head 所指向的子链表进行翻转，直到结尾，我们就得到了答案。下面我们该返回函数值了。

有的同学可能发现这又是一件麻烦事：链表翻转之后，链表的头节点发生了变化，那么应该返回哪个节点呢？照理来说，前 k 个节点翻转之后，链表的头节点应该是第 k 个节点。那么要在遍历过程中记录第 k 个节点吗？但是如果链表里面没有 k 个节点，答案又还是原来的头节点。我们又多了一大堆循环和判断要写，太崩溃了！

等等！还记得我们创建了节点 pre 吗？这个节点一开始被连接到了头节点的前面，而无论之后链表有没有翻转，它的 next 指针都会指向正确的头节点。那么我们只要返回它的下一个节点就好了。至此，问题解决。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* hair = new ListNode();
        hair->next = head;
        ListNode* pre = hair;
        while(head){
            ListNode* tail = pre;
            // 查看剩余部分长度是否大于等于 k
            for(int i=0;i<k;i++){
                tail = tail->next;
                if(!tail){
                    return hair->next;
                }
            }
            ListNode* net = tail->next;
            // 这里是 C++17 的写法，也可以写成
            // pair<ListNode*, ListNode*> result = myReverse(head, tail);
            // head = result.first;
            // tail = result.second;
            tie(head,tail) = reverseList(head,tail);
            // 把子链表重新接回原链表
            pre->next = head;
            tail->next = net;
            pre = tail;
            head = net;
        }
        return hair->next;
    }
    // 头插法翻转链表
    pair<ListNode*,ListNode*> reverseList(ListNode* head,ListNode* tail){
        tail->next = nullptr;
        ListNode* nxt = head;
        ListNode* cur = head->next;
        ListNode* tmp;
        while(cur){
            tmp = cur->next;
            cur->next = nxt;
            nxt = cur;
            cur = tmp;
        }
        head->next = nullptr;
        return {tail,head};
    }
};

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode hair = new ListNode();
        hair.next = head;
        ListNode fast = hair, slow = hair;
        while(fast != null){
            int cnt = 0;
            while(fast != null && cnt < k){
                ++cnt;
                fast = fast.next;
            }
            if(fast == null){
                return hair.next;
            }
            ListNode pre = fast.next;
            fast.next = null;
            ListNode[] res = reverse(slow.next);
            slow.next = res[0];
            res[1].next = pre;
            slow = res[1];
            fast = res[1];
        }
        return hair.next;
    }
    private ListNode[] reverse(ListNode head){
        ListNode hair = new ListNode();
        ListNode tail = head;
        ListNode tmp = hair;
        while(head != null){
            tmp = head.next;
            head.next = hair.next;
            hair.next = head;
            head = tmp;
        }
        return new ListNode[]{hair.next, tail};
    }
}

时间复杂度 O(n)
空间复杂度 O(1)

25. K 个一组翻转链表*

题目链接

题目描述

解题思路

方法一：