题目链接

牛客网
LeetCode

题目描述

在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字是重复的，也不知道每个数字重复几次。请找出数组中任意一个重复的数字。

  1. Input:
  2. {2, 3, 1, 0, 2, 5}
  4. Output:
  5. 2

解题思路

要求时间复杂度 O(N)，空间复杂度 O(1)。因此不能使用排序的方法，也不能使用额外的标记数组。
对于这种数组元素在 [0, n-1] 范围内的问题，可以将值为 i 的元素调整到第 i 个位置上进行求解。本题要求找出重复的数字，因此在调整过程中，如果第 i 位置上已经有一个值为 i 的元素，就可以知道 i 值重复。
以 (2, 3, 1, 0, 2, 5) 为例，遍历到位置 4 时，该位置上的数为 2，但是第 2 个位置上已经有一个 2 的值了，因此可以知道 2 重复：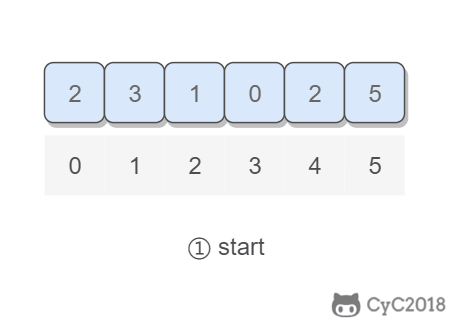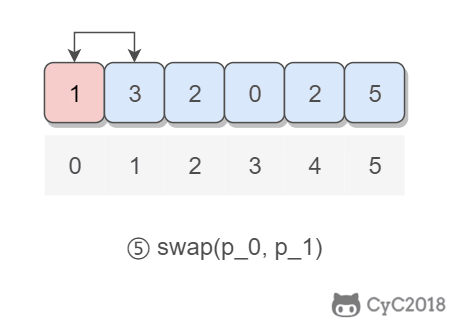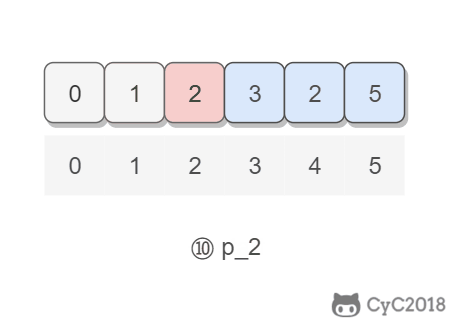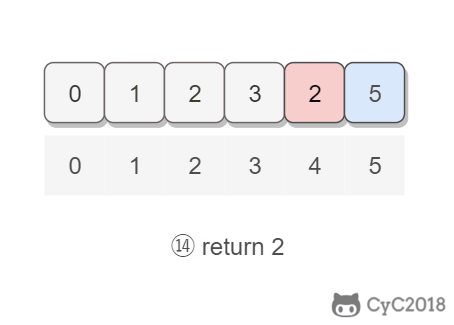
1.gif

方法一：哈希+遍历（因为不能用额外标记数组，所以不怎么好）

题目中含有重复的字眼，第一反应应该想到哈希，set。这里我们用哈希来解。
算法步骤：

  1. 开辟一个长度为n的vector, 初始化为false
  2. 遍历数组，第一次遇到的数据，对应置为true
  3. 如果再一次遇到已经置为true的数据，说明是重复的。返回即可。

代码如下：

  1. class Solution {
  2. public:
  3.     // Parameters:
  4.     //        numbers:     an array of integers
  5.     //        length:      the length of array numbers
  6.     //        duplication: (Output) the duplicated number in the array number
  7.     // Return value:       true if the input is valid, and there are some duplications in the array number
  8.     //                     otherwise false
  9.     bool duplicate(int numbers[], int length, int* duplication) {
  10.         vector<bool> f(length, false);
  11.         for (int i=0; i<length; ++i) {
  12.             if (!f[numbers[i]]) {
  13.                 f[numbers[i]] = true;
  14.             }
  15.             else {
  16.                 *duplication = numbers[i];
  17.                 return true;
  18.             }
  19.         }
  20.         return false;
  21.     }
  22. };
class Solution {
    public List<Integer> findDuplicates(int[] nums) {
        boolean[] arr = new boolean[nums.length+1];
        List<Integer> res = new ArrayList<>();
        for(int n: nums){
            if(arr[n]){
                res.add(n);
            }else{
                arr[n] = true;
            }
        }
        return res;
    }
}
  • 时间复杂度：O(N)
  • 空间复杂度：O(N)

    方法二：in-place算法（同第一种，再加上判断数组是否有效最好）

    方法一中的一个条件我们没有用到。也就是数据的范围是0-n-1。所以我们可以这么做：
  1. 设置一个指针i指向开头0，
  2. 对于arr[i]进行判断，如果arr[i] == i， 说明下标为i的数据正确的放在了该位置上，让i++
  3. 如果arr[i] != i, 说明没有正确放在位置上，那么我们就把arr[i]放在正确的位置上，也就是交换
    arr[i] 和arr[arr[i]]。交换之后，如果arr[i] ！= i, 继续交换。
  4. 如果交换的过程中，arr[i] == arr[arr[i]]，说明遇到了重复值，返回即可。
    如下图：

image.png

class Solution {
public:
 // Parameters:
 //        numbers:     an array of integers
 //        length:      the length of array numbers
 //        duplication: (Output) the duplicated number in the array number
 // Return value:       true if the input is valid, and there are some duplications in the array number
 //                     otherwise false
 bool duplicate(int numbers[], int length, int* duplication) {
     for (int i=0; i<length; ++i) {
         // 不相等就一直交换
         while (i != numbers[i]) {
             if (numbers[i] != numbers[numbers[i]]) {
                 swap(numbers[i], numbers[numbers[i]]);
             }
             else {
                 *duplication = numbers[i];
                 return true;
             }
         }

     }
     return false;
 }
};
  • 时间复杂度：O(N)
  • 空间复杂度：O(1)