题目链接

牛客网

题目描述

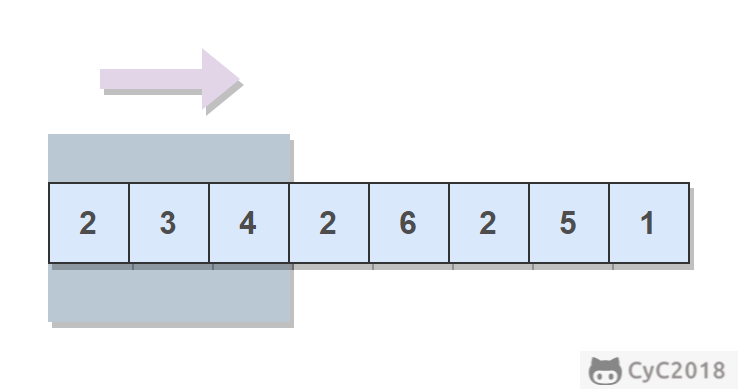
给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。
窗口大于数组长度的时候，返回空

示例

  1. // 输入
  2. [2,3,4,2,6,2,5,1],3
  4. // 输出
  5. [4,4,6,6,6,5]

59.1 滑动窗口的最大值 - 图1

解题思路

方法一：暴力方法

算法步骤如下：

  • 枚举每个窗口的左边界 i
  • 根据窗口的左边界i可以对应计算出右边界j
  • 遍历窗口，计算出最大值
class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        vector<int> ret;
        if (num.size() == 0 || size < 1 || num.size() < size) return ret;
        int n = num.size();

        for (int i = 0; i + size - 1 < n; ++i) {
            int j = i + size - 1;
            int max_val = num[j];
            for (int k = i; k < j; ++k) {
                max_val = max(max_val, num[k]);
            }
            ret.push_back(max_val);
        }
        return ret;
    }
};
  • 时间复杂度：O(n*k), 其中n为数组大小，k为窗口大小
  • 空间复杂度：O(1)，存结果必须要开的数组不算入额外空间

方法二：单调队列

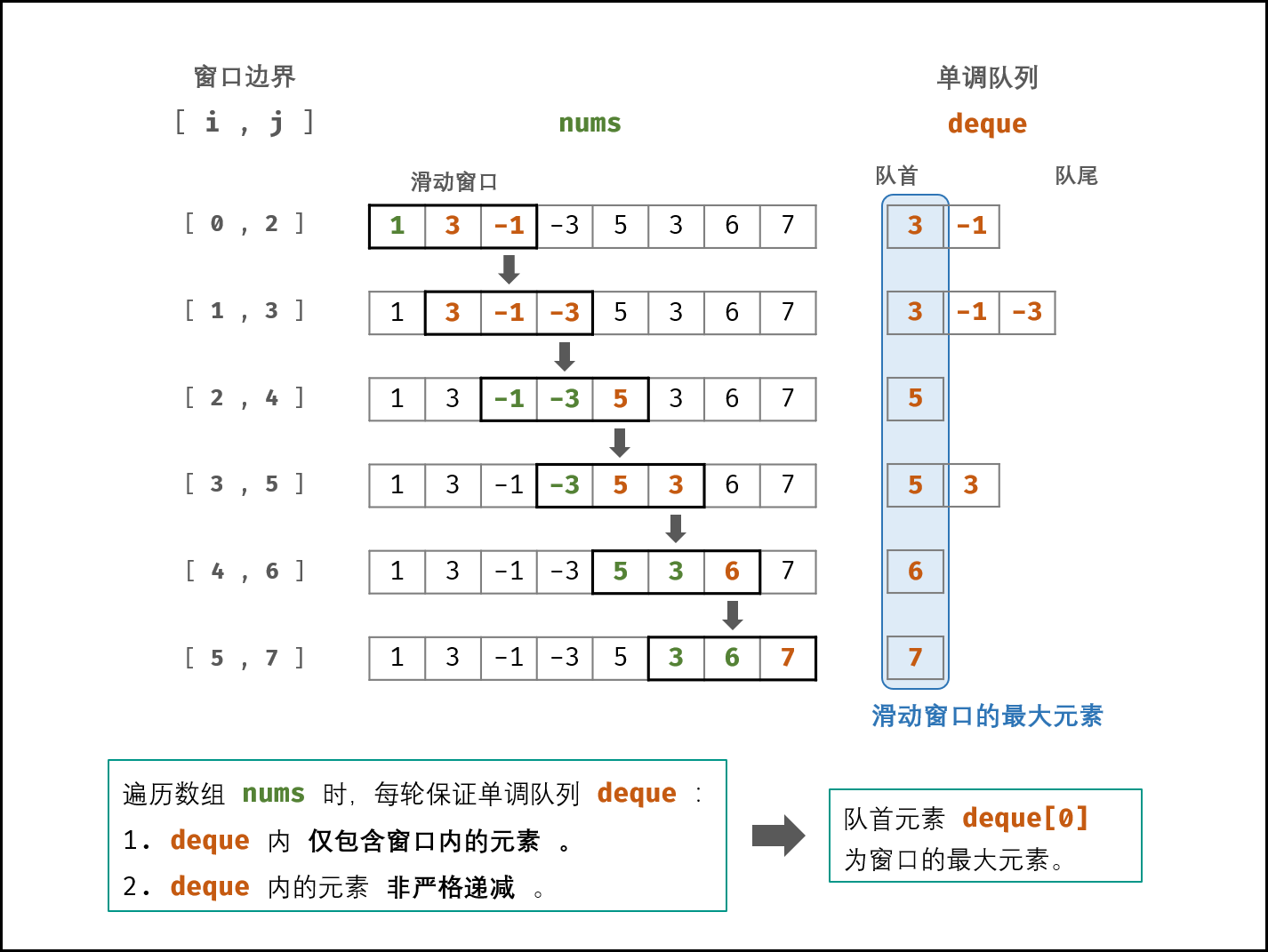
59.1 滑动窗口的最大值 - 图2

  1. 初始化： 双端队列 deque，结果列表 res ，数组长度 n ；
  2. 滑动窗口： 左边界范围i∈[1−k,n+1−k] ，右边界范围j∈[0,n−1] ；

1.若 i>0 且 队首元素deque[0] = 被删除（移出移动窗口）元素 nums[i−1] ：则队首元素出队；
2.删除 deque 内所有3.将 nums[j] 添加至 deque 尾部；
4.若已形成窗口（即 i≥0 ）：将窗口最大值（即队首元素deque[0] ）添加至列表res 。

  1. 返回值： 返回结果列表 res 。

总结一下，首先容器中放的元素应该是单调递减的。然后还有删除容器头部元素和最后一个元素的操作。因此，这样的数据结构就是双端队列。c++中就是deque

class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        // 判断特殊情况
        int n = num.size();
        if(n < size || size <= 0) return {};
        deque<int> dq;//双端队列
        vector<int> res;
        // i为左指针 j为👉右指针
        // i=[1−size,n+1−size] j=[0,n-1]
        for(int i = 1-size,j=0;j<n;++i,++j){
            // 被移出滑动窗口的是当前窗口最大值并且是应该划出窗口的值
            if(i>0&&dq[0]==num[i-1])
                dq.pop_front();
            // 删除 deque 内所有 <nums[j] 的元素，以保持 deque递减；
            while(!dq.empty()&&dq.back()<num[j])
                dq.pop_back();
            // 将 nums[j] 添加至 deque 尾部
            dq.push_back(num[j]);
            // 若已形成窗口（即i≥0）：将窗口最大值（即队首元素 deque[0] ）添加至列表 res 。
            if(i>=0)
                res.push_back(dq[0]);
        }
        return res;
    }
};

方法三：堆

维护一个大小为窗口大小的大顶堆，顶堆元素则为当前窗口的最大值。

假设窗口的大小为 M，数组的长度为 N。在窗口向右移动时，需要先在堆中删除离开窗口的元素，并将新到达的元素添加到堆中，这两个操作的时间复杂度都为 log2M，因此算法的时间复杂度为 O(Nlog2M)，空间复杂度为 O(M)。

public ArrayList<Integer> maxInWindows(int[] num, int size) {
    ArrayList<Integer> ret = new ArrayList<>();
    if (size > num.length || size < 1)
        return ret;
    PriorityQueue<Integer> heap = new PriorityQueue<>((o1, o2) -> o2 - o1);  /* 大顶堆 */
    for (int i = 0; i < size; i++)
        heap.add(num[i]);
    ret.add(heap.peek());
    for (int i = 0, j = i + size; j < num.length; i++, j++) {            /* 维护一个大小为 size 的大顶堆 */
        heap.remove(num[i]);
        heap.add(num[j]);
        ret.add(heap.peek());
    }
    return ret;
}