题目链接

LeetCode

题目描述

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1：

输入： nums1 = [1,3], nums2 = [2]
输出： 2.00000
解释： 合并数组 = [1,2,3] ，中位数 2

示例 2：

输入： nums1 = [1,2], nums2 = [3,4]
输出： 2.50000
解释： 合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：

输入： nums1 = [0,0], nums2 = [0,0]
输出： 0.00000

示例 4：

输入： nums1 = [], nums2 = [1]
输出： 1.00000

示例 5：

输入： nums1 = [2], nums2 = []
输出： 2.00000

提示：

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000
  • -106 <= nums1[i], nums2[i] <= 106

进阶： 你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

解题思路

方法一：合并数组法

  1. class Solution {
  2.     public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  3.         int len = nums1.length + nums2.length;
  4.         int[] nums = new int[len];
  5.         int i = 0, j = 0, pos = 0;
  6.         while(i < nums1.length && j < nums2.length){
  7.             if(nums1[i] < nums2[j]){
  8.                 nums[pos++] = nums1[i++];
  9.             }else{
  10.                 nums[pos++] = nums2[j++];
  11.             }
  12.         }
  13.         while(i < nums1.length){
  14.             nums[pos++] = nums1[i++];
  15.         }
  16.         while(j < nums2.length){
  17.             nums[pos++] = nums2[j++];
  18.         }
  19.         return (nums[(len - 1) / 2] + nums[len/2])*1.0/2;
  20.     }
  21. }
  • 时间复杂度 O(n)
  • 空间复杂度 O(n)

方法二：二分查找

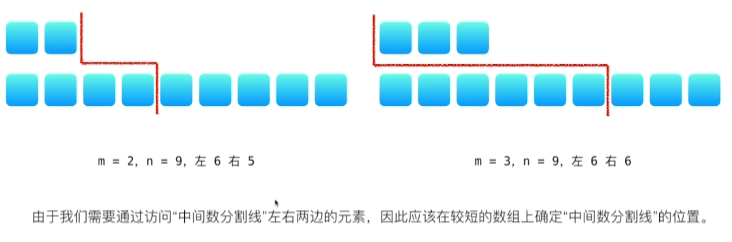
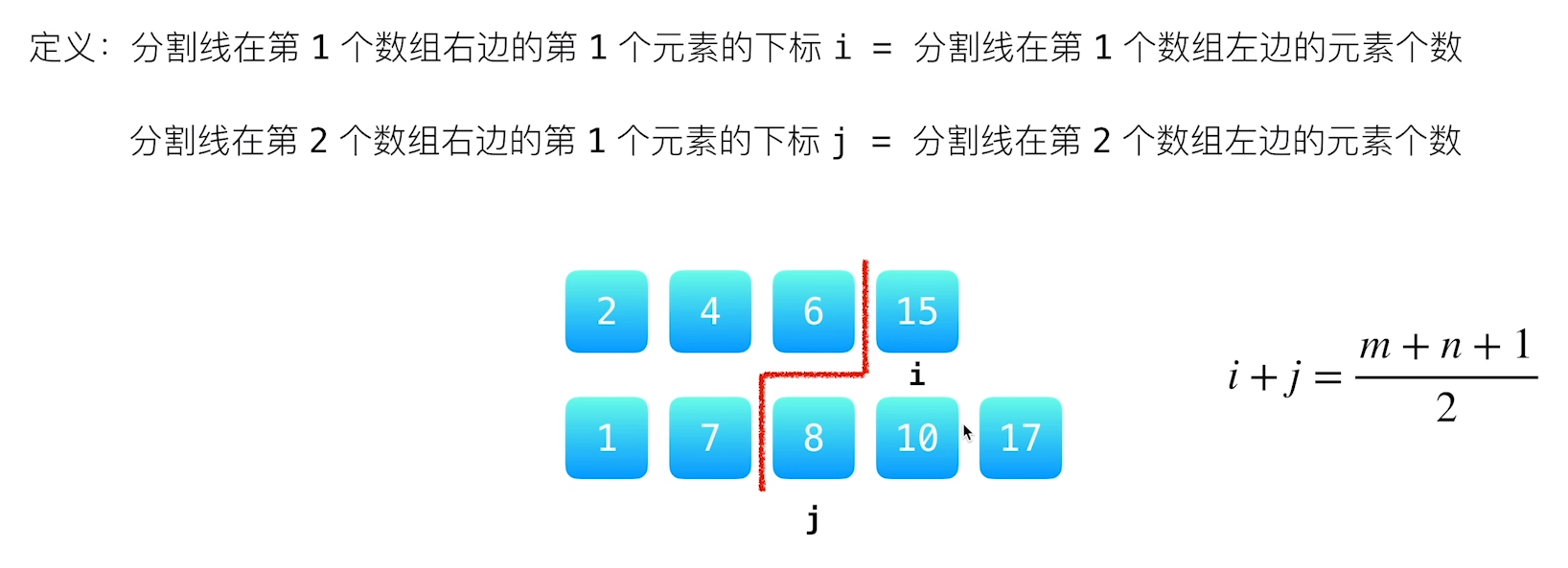
image.png
image.png
image.png

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        // 保证num1是短的数组
        if(nums1.length > nums2.length){
            int[] tmp = nums1;
            nums1 = nums2;
            nums2 = tmp;
        }
        int m = nums1.length;
        int n = nums2.length;
        // 分割线左边的所有元素需要满足的个数 m + (n - m + 1)/2  当为奇数个时，左边多一个;
        // 加一奇数时左边多一个
        int totalLeft = (m + n + 1)/2;

        // 在 nums1 的区间[0, m]里查找恰当的分割线
        // 使得 num1[i-1] <= nums2[j] && num2[j-1] <= nums1[i]
        int left = 0;
        int right = m; // right = m 可以将分割线划到Num1最右边
        while(left < right){
            // 加一为了避免当left == i 只剩下两个元素时产生死循环 
            // 这样中位数 i 也取不到 0  nums1[i-1] 不会越界
            // i 是 nums1左边元素的个数，也是 分割线右边元素的下标
            int i = left + (right - left + 1) / 2;
            // j 是 Num2左边元素的个数，也是 分割线右边元素的下标
            int j = totalLeft - i;
            if(nums1[i-1] > nums2[j]){
                // 下一轮搜索的区间 [left, i - 1]
                right = i - 1;
            }else{
                // 下一轮搜索的区间 [i, right]
                left = i;
            }
        }
        // 最后划分的分割线
        int i = left;
        int j = totalLeft - i;
           // 判断是否是极端情况
        int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i-1];
        int nums1RightMin = i == m ? Integer.MAX_VALUE : nums1[i];
        int nums2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j-1];
        int nums2RightMin = j == n ? Integer.MAX_VALUE : nums2[j];
        if((m+n)%2 == 1){
            return Math.max(nums1LeftMax, nums2LeftMax);
        }else{
            return ((double)Math.max(nums1LeftMax, nums2LeftMax) + (double)Math.min(nums1RightMin, nums2RightMin))/2;
        }
    }
}
  • 时间复杂度 O(log(m+n))
  • 空间复杂度 O(1)