题目链接

LeetCode

题目描述

给你一个字符串 s，找到 s 中最长的回文子串。

解题思路

方法一：动态规划

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.length();
        if(len<2)
            return s;
        int begin = 0;
        int maxLen = 1;
        vector<vector<bool>> dp(len,vector<bool>(len,false));
        for(int i=0;i<len;++i){
            dp[i][i] = true;
        }
        for(int j = 1;j<len;++j){
            for(int i = 0;i<j;++i){
                if(s[i]==s[j]){
                    if(j-i<3){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i+1][j-1];
                    }
                }
                if(dp[i][j]&&j-i+1>maxLen){
                    maxLen = j-i+1;
                    begin = i;
                }
            }
        }
        return s.substr(begin,maxLen);
    }
};

• 时间复杂度 O(n^2)
• 空间复杂度 O(n^2)

方法二：中心扩展算法

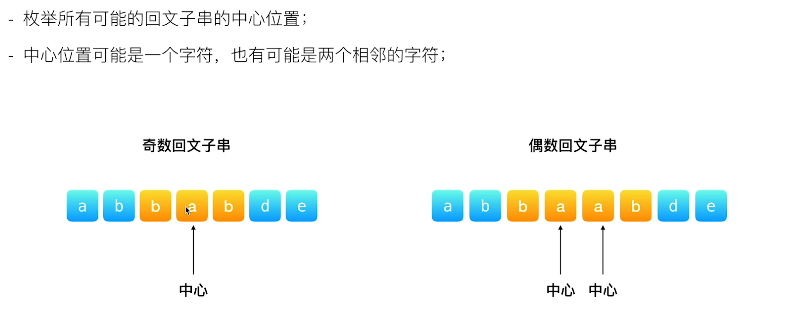
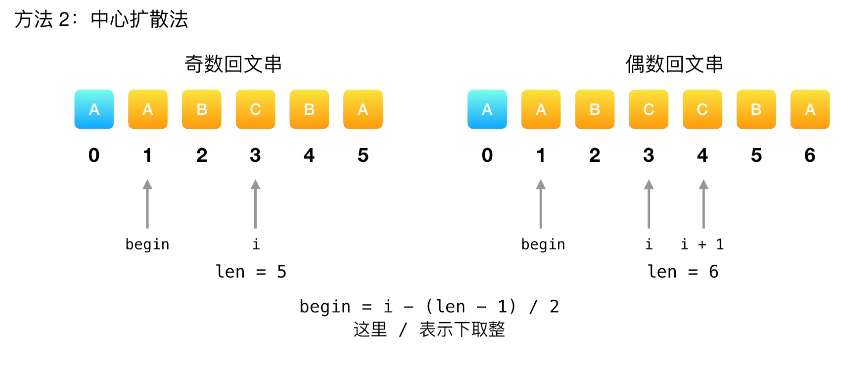
class Solution {
public:
    string longestPalindrome(string s) {
        this->len = s.length();
        if(len<2){
            return s;
        }
        str = s;
        //最长回文串的长度
        int max_len = 0;
        //最长回文串的开始位置
        int begin = -1;
        string res = "";
        for(int i = 0;i<len-1;i++){
            int tmp = max(expandAround(i,i),expandAround(i,i+1));
            if(tmp>max_len){
                max_len = tmp;
                //计算得出开始位置，maxLen-1可以考虑maxLen为偶数的情况
                begin = i - (max_len-1)/2;
            }  
        }
        return s.substr(begin,max_len);
    }
private:
    string str = "";
    int len = 0;
    int expandAround(int left,int right){
        while(left>=0&&right<len){
            if(str[left]!=str[right]){
                break;
            }
            left--;
            right++;
        }
        return right-left-1;
    }
};

• 时间复杂度 O(n^2)
• 空间复杂度 O(1)