题目链接

LeetCode

题目描述

给定一个二叉树，确定它是否是一个完全二叉树。

百度百科中对完全二叉树的定义如下：

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（注：第 h 层可能包含 1~ 2h 个节点。）

示例 1：

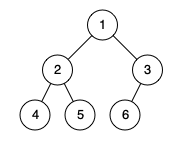
输入： [1,2,3,4,5,6]
输出： true
解释： 最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。

示例 2：

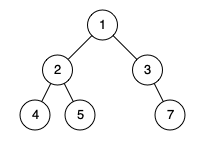
输入： [1,2,3,4,5,null,7]
输出： false
解释： 值为 7 的结点没有尽可能靠向左侧。

解题思路

方法一：广度优先搜索

什么时候是不完全呢？其实就是出现null结点之后后面又出现了结点，如果是完全则最后一个null结点之后就结束遍历了

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isCompleteTree(TreeNode* root) {
        // 层序遍历的辅助利器
        queue<TreeNode*> q;
        // 记录是否已经遍历到null结果
        bool reachNull = false;
        q.push(root);
        while (!q.empty()){
            TreeNode* curr = q.front();
            q.pop();
            if (curr == nullptr){
                // 发现空结点了
                reachNull = true;
                continue;
            }else{
                // 发现null结点后出现非空结点，发现不完全了
                if (reachNull){
                    return false;
                }
                // 继续遍历左右节点
                q.push(curr->left);
                q.push(curr->right);
            }
        }
        return true;
    }
};

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isCompleteTree(TreeNode root) {
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(root);
        boolean searchNull = false; // 遇到null了吗
        while(!q.isEmpty()){
            TreeNode node = q.poll();
            if(node == null){
                searchNull = true;
            }else{
                if(searchNull){
                    return false;
                }
                q.offer(node.left);
                q.offer(node.right);
            }
        }
        return true;
    }
}

• 时间复杂度 O(n)
• 空间复杂度 O(2^k)

  方法二：数组

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isCompleteTree(TreeNode root) {
        List<TreeNode> lst = new ArrayList<TreeNode>();
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        q.offer(root);
        while(!q.isEmpty()){
            TreeNode node = q.poll();
            if(node != null){
                q.offer(node.left);
                q.offer(node.right);
            }
            lst.add(node);
        }
        int i = 0;
        while(i < lst.size()){
            if(lst.get(i) == null || lst.get(2*i + 1) == null || lst.get(2*i + 2) == null){
                if(lst.get(i) == null){
                    break;
                }else if(lst.get(2*i + 1) == null){
                    i = 2*i + 1;
                }else{
                    i = 2*i + 2;
                }
                break;
            }
            ++i;
        }
        while(i < lst.size()){
            if(lst.get(i++) != null){
                return false;
            }
        }
        return true;
    }
}