题目链接

LeetCode
LeetCode变形

题目描述

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：

输入： nums = [4,5,6,7,0,1,2], target = 0
输出： 4

示例 2：

输入： nums = [4,5,6,7,0,1,2], target = 3
输出： -1

示例 3：

输入： nums = [1], target = 0
输出： -1

解题思路

方法一：二分查找

对于有序数组，可以使用二分查找的方法查找元素。

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环.

但是这道题中，数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，这还能进行二分查找吗？答案是可以的。
可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。
这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分：
如果 [l, mid - 1] 是有序数组，且 target 的大小满足[nums[l],nums[mid])，则我们应该将搜索范围缩小至 [l, mid - 1]，否则在 [mid + 1, r] 中寻找。
如果 [mid, r] 是有序数组，且 target 的大小满足](nums[mid+1],nums[r]]，则我们应该将搜索范围缩小至 [mid + 1, r]，否则在 [l, mid - 1] 中寻找。

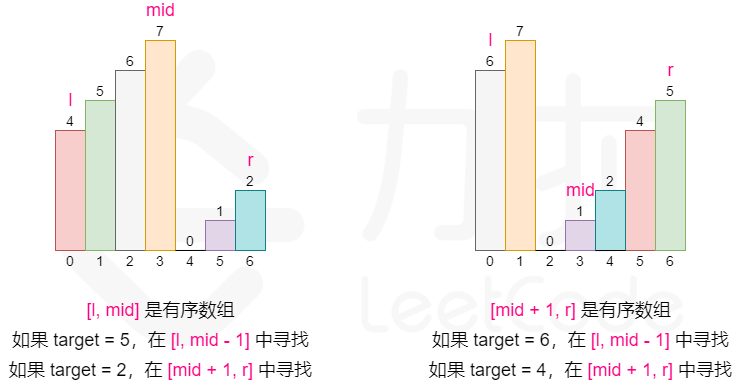
33. 搜索旋转排序数组*** - 图1
需要注意的是，二分的写法有很多种，所以在判断 target 大小与有序部分的关系的时候可能会出现细节上的差别

代码：

  1. class Solution {
  2.     public int search(int[] nums, int target) {
  3.         int len = nums.length;
  4.         if(len == 0){
  5.             return -1;
  6.         }
  7.         if(len == 1){
  8.             return nums[0] == target ? 0 : -1;
  9.         }
  10.         int left = 0, right = len - 1;
  11.         while(left <= right){
  12.             int mid = left + (right - left) / 2;
  13.             if(nums[mid] == target){
  14.                 return mid;
  15.             }
  16.             if(nums[mid] >= nums[0]){
  17.                 if(nums[left] <= target && target < nums[mid]){
  18.                     right = mid - 1;
  19.                 }else{
  20.                     left = mid + 1;
  21.                 }
  22.             }else{
  23.                 if(nums[mid] < target && target <= nums[right]){
  24.                     left = mid + 1;
  25.                 }else{
  26.                     right = mid - 1;
  27.                 }
  28.             }
  29.         }
  30.         return -1;
  31.     }
  32. }
  • 时间复杂度：O(log n)
  • 空间复杂度：O(1)

    变形题：如果数组中的值不唯一

也就是会出现[3, 4, 5, 6, 1, 2, 3, 3, 3]这种情况

对于数组中有重复元素的情况，二分查找时可能会有 a[l]=a[mid]=a[r]，此时无法判断区间 [l,mid] 和区间 [mid+1,r] 哪个是有序的。

例如 nums=[3,1,2,3,3,3,3]，target=2，首次二分时无法判断区间 [0,3] 和区间 [4,6] 哪个是有序的。

对于这种情况，我们只能将当前二分区间的左边界加一，右边界减一，然后在新区间上继续二分查找。

class Solution {
    public boolean search(int[] nums, int target) {
        int len = nums.length;
        if(len == 0){
            return false;
        }
        if(len == 1){
            return nums[0] == target;
        }
        int left = 0, right = len - 1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                return true;
            }
            if(nums[left] == nums[mid] && nums[right] == nums[mid]){
                ++left;
                --right;
            }else if(nums[mid] >= nums[left]){
                if(nums[left] <= target && target < nums[mid]){
                    right = mid - 1;
                }else{
                    left = mid + 1;
                }
            }else{
                if(nums[mid] < target && target <= nums[right]){
                    left = mid + 1;
                }else{
                    right = mid - 1;
                }
            }
        }
        return false;
    }
}
  • 时间复杂度：O(log n)
  • 空间复杂度：O(1)

    变形二：旋转多次

    如果面试官问你再旋转一次怎么做，做法还是一样的，无论旋转几次，最多只有2段递增序列。