题目链接

LeetCode

题目描述

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例 1:

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

解题思路

方法一：动态规划

考虑当前位置如果是一个负数的话，那么我们希望以它前一个位置结尾的某个段的积也是个负数，这样就可以负负得正，并且我们希望这个积尽可能「负得更多」，即尽可能小。如果当前位置是一个正数的话，我们更希望以它前一个位置结尾的某个段的积也是个正数，并且希望它尽可能地大。于是这里我们可以再维护一个 fmin(i)，它表示以第 i 个元素结尾的乘积最小子数组的乘积，那么我们可以得到这样的动态规划转移方程：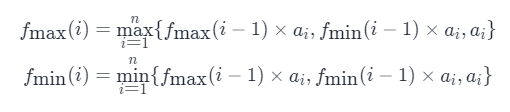
image.png
它代表第 i 个元素结尾的乘积最大子数组的乘积 fmax(i)，可以考虑把 a_i 加入第 i−1 个元素结尾的乘积最大或最小的子数组的乘积中，二者加上 a_i ，三者取大，就是第 i 个元素结尾的乘积最大子数组的乘积。第 i 个元素结尾的乘积最小子数组的乘积 fmin(i) 同理。

  1. class Solution {
  2.     public int maxProduct(int[] nums) {
  3.         int[] Fmax = new int[nums.length];
  4.         int[] Fmin = new int[nums.length];
  5.         Fmax[0] = Fmin[0] = nums[0];
  6.         int ans = Fmax[0];
  7.         for(int i = 1; i < nums.length; ++i){
  8.             Fmax[i] = Math.max(Fmax[i-1] * nums[i], Math.max(Fmin[i-1] * nums[i], nums[i]));
  9.             Fmin[i] = Math.min(Fmax[i-1] * nums[i], Math.min(Fmin[i-1] * nums[i], nums[i]));
  10.             ans = Math.max(ans, Fmax[i]);
  11.         }
  12.         return ans;
  13.     }
  14. }

空间优化后

class Solution {
    public int maxProduct(int[] nums) {
        int Fmax = nums[0];
        int Fmin = nums[0];
        int ans = nums[0];
        int tmp = 0;
        for(int i = 1; i < nums.length; ++i){
            tmp = Fmax;
            Fmax = Math.max(Fmax * nums[i], Math.max(Fmin * nums[i], nums[i]));
            Fmin = Math.min(tmp * nums[i], Math.min(Fmin * nums[i], nums[i]));
            ans = Math.max(ans, Fmax);
        }
        return ans;
    }
}
  • 时间复杂度 O(n)
  • 空间复杂度 O(n) 空间优化后为O(1)