题目链接

LeetCode

题目描述

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。
例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

1<br />   / \<br />   2   2<br />    / \ / \<br />     3  4 4  3<br />但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1<br />   / \<br />    2   2<br />     \   \<br />         3    3<br />示例：

输入：root = [1,2,2,3,4,4,3]
输出：true

输入：root = [1,2,2,null,3,null,3]
输出：false

解题思路

递归

分析过程

对称二叉树定义： 对于树中 任意两个对称节点 L 和 R ，一定有：

• L.val=R.val ：即此两对称节点值相等。
• L.left.val=R.right.val ：即 L 的 左子节点 和 R 的 右子节点 对称；
• L.right.val=R.left.val ：即 L 的 右子节点 和 R 的 左子节点 对称。

根据以上规律，考虑从顶至底递归，判断每对节点是否对称，从而判断树是否为对称二叉树。

算法流程：

isSymmetric(root) ：

特例处理： 若根节点 root 为空，则直接返回 true 。
返回值： 即 recur(root.left, root.right) ;

recur(L, R) ：

终止条件：

• 当 L 和 R 同时越过叶节点： 此树从顶至底的节点都对称，因此返回 true ；
• 当 L 或 R 中只有一个越过叶节点： 此树不对称，因此返回 false ；
• 当节点 L 值 != 节点 R 值： 此树不对称，因此返回 false ；

递推工作：

• 判断两节点 L.left 和 R.right 是否对称，即 recur(L.left, R.right) ；
• 判断两节点 L.right 和 R.left 是否对称，即 recur(L.right, R.left) ；

返回值：

• 两对节点都对称时，才是对称树，因此用与逻辑符 && 连接

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        // 当树为空时，一定是对称二叉树
        if(root==NULL) return true;
        return recur(root->left,root->right);
    }
private:
    bool recur(TreeNode* left,TreeNode* right){
        // 当 L 和 R 同时越过叶节点： 此树从顶至底的节点都对称，因此返回 true ；
        if(left==NULL&&right==NULL) return true;
        // 当 L 或 R 中只有一个越过叶节点： 此树不对称，因此返回 false ；
        if(left==NULL||right==NULL) return false;
        // 当节点 L 值  != 节点 R 值： 此树不对称，因此返回 false ；
        if(left->val!=right->val) return false;
        // 判断两节点 L.left 和 R.right 是否对称，即 recur(L.left, R.right) ；
        // 判断两节点 L.right 和 R.left 是否对称，即 recur(L.right, R.left) ；
        // 两对节点都对称时，才是对称树，因此用与逻辑符 && 连接
        return recur(left->left,right->right)&&recur(left->right,right->left);
    }
};

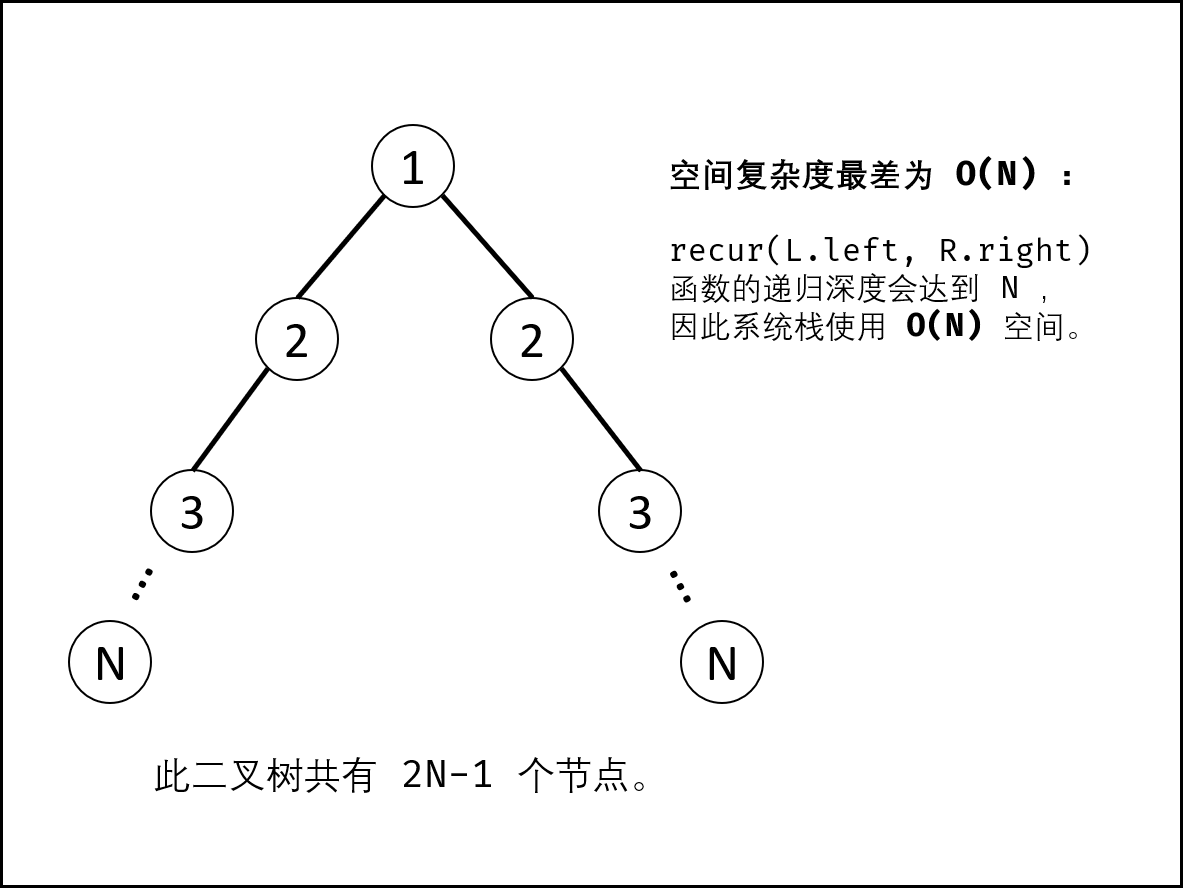
• 时间复杂度 O(N) ： 其中 N 为二叉树的节点数量，每次执行 recur() 可以判断一对节点是否对称，因此最多调用 N/2 次 recur() 方法。
• 空间复杂度 O(N) ： 最差情况下（见下图），二叉树退化为链表，系统使用 O(N) 大小的栈空间。