题目链接

牛客网

题目描述

一个链表中包含环，请找出该链表的环的入口结点。要求不能使用额外的空间。

解题思路

方法一：哈希法

1. 遍历单链表的每个结点
2. 如果当前结点地址没有出现在set中，则存入set中
3. 否则，出现在set中，则当前结点就是环的入口结点

4. 整个单链表遍历完，若没出现在set中，则不存在环

   /*
   struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
   };
   */
   class Solution {
   public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        unordered_set<ListNode*> st;
        while(pHead){
            if(st.find(pHead)==st.end()){
                st.insert(pHead);
                pHead = pHead->next;
            }else{
                return pHead;
            }
        }
        return nullptr;
    }
   };

   时间复杂度：O(n)
   空间复杂度：O(n)，最坏情况下，单链表的所有结点都在存入set

   方法二：双指针(快慢指针)

5. 初始化：快指针fast指向头结点， 慢指针slow指向头结点

6. 让fast一次走两步， slow一次走一步，第一次相遇在C处，停止
7. 然后让fast指向头结点，slow原地不动
8. 最后fast，slow每次走一步，当再次相遇，就是入口结点。

解释：

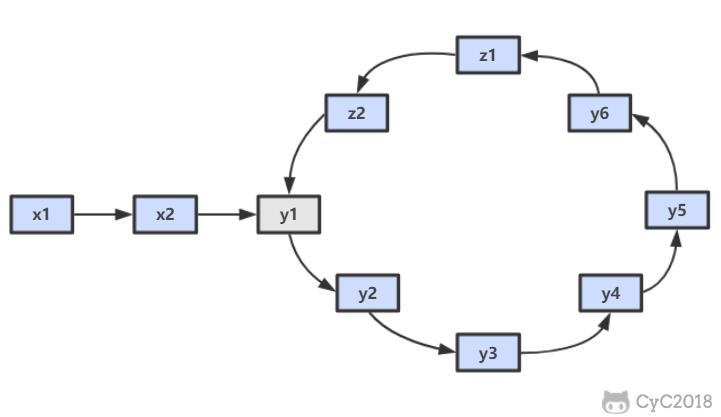
假设环入口节点为 y1，相遇所在节点为 z1。

假设快指针 fast 在圈内绕了 N 圈，则总路径长度为 x+Ny+(N-1)z。z 为 (N-1) 倍是因为快慢指针最后已经在 z1 节点相遇了，后面就不需要再走了。

而慢指针 slow 总路径长度为 x+y。

因为快指针是慢指针的两倍，因此 x+Ny+(N-1)z = 2(x+y)。

我们要找的是环入口节点 y1，也可以看成寻找长度 x 的值，因此我们先将上面的等值分解为和 x 有关：x=(N-2)y+(N-1)z。

上面的等值没有很强的规律，但是我们可以发现 y+z 就是圆环的总长度，因此我们将上面的等式再分解：x=(N-2)(y+z)+z。这个等式左边是从起点 x1 到环入口节点 y1 的长度，而右边是在圆环中走过 (N-2) 圈，再从相遇点 z1 再走过长度为 z 的长度。此时我们可以发现如果让两个指针同时从起点 x1 和相遇点 z1 开始，每次只走过一个距离，那么最后他们会在环入口节点相遇。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        if(pHead==nullptr||pHead->next==nullptr)
            return nullptr;
        ListNode*fast=pHead,*slow=pHead;
        do{
            fast = fast->next->next;
            slow = slow->next;
        }while(fast!=nullptr&&fast!=slow);
        if(fast==nullptr) return nullptr;
        fast = pHead;
        while(slow!=fast){
            slow = slow->next;
            fast = fast->next;
        }
        return fast;
    }
};

• 时间复杂度：O(n)
• 空间复杂度：O(1)