题目链接

LeetCode

题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

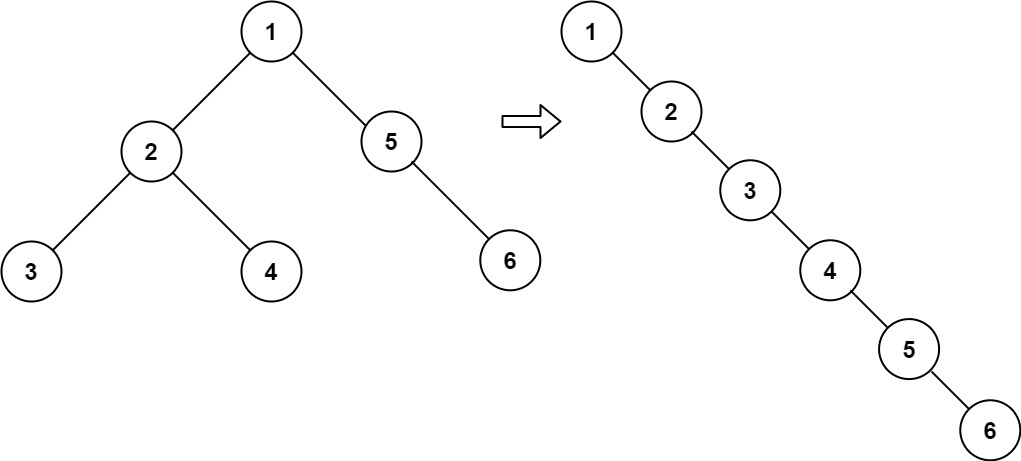
输入： root = [1,2,5,3,4,null,6]
输出： [1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入： root = []
输出： []

示例 3：

输入： root = [0]
输出： [0]

提示：

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

进阶： 你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

解题思路

方法一：前序遍历

将二叉树展开为单链表之后，单链表中的节点顺序即为二叉树的前序遍历访问各节点的顺序。因此，可以对二叉树进行前序遍历，获得各节点被访问到的顺序。由于将二叉树展开为链表之后会破坏二叉树的结构，因此在前序遍历结束之后更新每个节点的左右子节点的信息，将二叉树展开为单链表。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        if(root==nullptr)
            return;
        recur(root);
        int n = vec.size();
        for(int i=0;i<n-1;i++){
            vec[i]->right = vec[i+1];
            vec[i]->left = nullptr;
        }
    }
    void recur(TreeNode* root){
        if(root==nullptr)
            return;
        vec.push_back(root);
        recur(root->left);
        recur(root->right);
    }
private:
    vector<TreeNode*> vec;
};

• 时间复杂度 O(n)
• 空间复杂度 O(n)

方法二：寻找前驱节点

注意到前序遍历访问各节点的顺序是根节点、左子树、右子树。

• 如果一个节点的左子节点为空，则该节点不需要进行展开操作。
• 如果一个节点的左子节点不为空，则该节点的左子树中的最后一个节点被访问之后，该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点，也是该节点的前驱节点。

因此，问题转化成寻找当前节点的前驱节点。

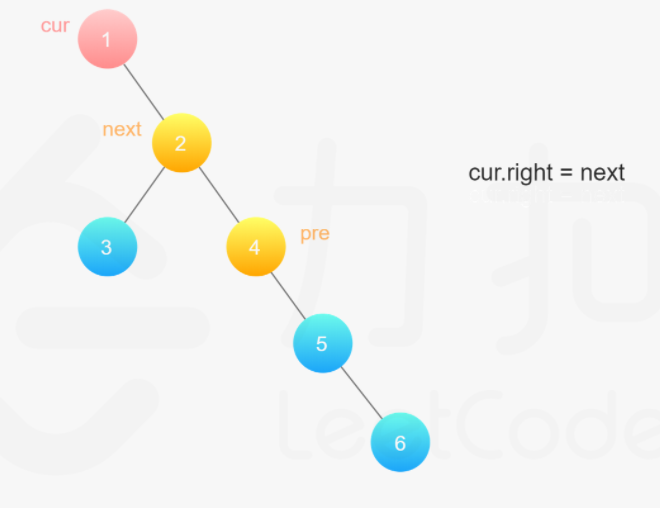
具体做法是
对于当前节点，如果其左子节点不为空，

• 则在其左子树中找到最右边的节点，作为前驱节点，
• 将当前节点的右子节点赋给前驱节点的右子节点，
• 然后将当前节点的左子节点赋给当前节点的右子节点，并将当前节点的左子节点设为空。
• 对当前节点处理结束后，继续处理链表中的下一个节点，直到所有节点都处理结束。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        if(root==nullptr)
            return;
        TreeNode* cur = root;
        while(cur!=nullptr){
            if(cur->left!=nullptr){
                // 中序遍历下一个结点为左子树结点
                TreeNode* next = cur->left;
                // 找出左子树最右边结点，也是中序遍历左子树最后一个结点
                TreeNode* pre = next;
                while(pre->right!=nullptr){
                    pre = pre->right;
                }
                // 中序遍历左子树最后一个结点的右子树指向右子树第一个结点（连接左右子树结点链表）
                pre->right = cur->right;
                // 当前结点的左子树设为null，右子树指向下一个结点（左子树第一个结点）
                cur->left = nullptr;
                cur->right = next;
            }
            // 指向下一个中序遍历结点
            cur = cur->right;
        }
    }
};

• 时间复杂度 O(n)
• 空间复杂度 O(1)