题目链接

LeetCode

题目描述

给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入： lists = [[1,4,5],[1,3,4],[2,6]]
输出： [1,1,2,3,4,4,5,6]
解释： 链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入： lists = []
输出： []

示例 3：

输入： lists = [[]]
输出： []

提示：

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] 按 升序 排列
• lists[i].length 的总和不超过 10^4

  解题思路

  方法一：两两链表合并、空间复杂度低

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int len = lists.size();
        ListNode* ans = nullptr;
        for(int i = 0;i<len;i++){
            ans = merge2Lists(ans,lists[i]);
        }
        return ans;
    }
    ListNode* merge2Lists(ListNode* list1,ListNode* list2){
        ListNode* hair = new ListNode();
        ListNode* cur = hair;
        while(list1&&list2){
            if(list1->val<list2->val){
                cur->next = list1;
                cur = cur->next;
                list1 = list1->next;
            }else{
                cur->next = list2;
                cur = cur->next;
                list2 = list2->next;
            }
        }
        if(list1){
            cur->next = list1;
        }
        if(list2){
            cur->next = list2;
        }
        return hair->next;
    }
};

• 时间复杂度 O(k^2n)：k为链表个数

• 空间复杂度 O(1)

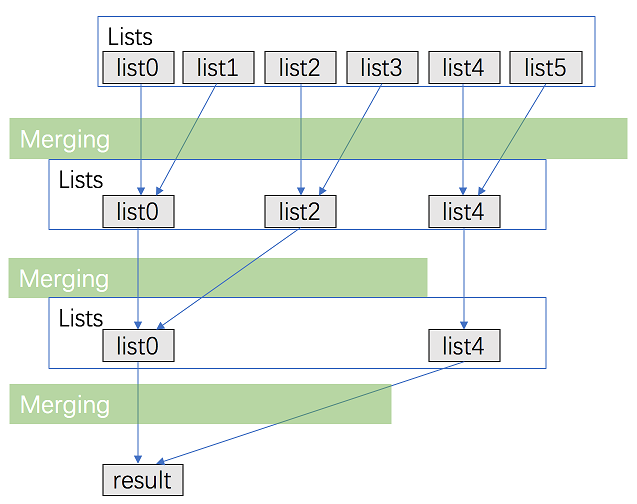
  方法二：分治合并、方法一的优化，时间复杂度小

  考虑优化方法一，用分治的方法进行合并。

• 将 k 个链表配对并将同一对中的链表合并；

• 第一轮合并以后， k 个链表被合并成了 k/2 个链表，平均长度为 2*n/k ，然后是 k/4 个链表，k/8 个链表等等；
• 重复这一过程，直到我们得到了最终的有序链表。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return merge(lists,0,lists.size()-1);
    }
    ListNode* merge(vector <ListNode*> &lists, int l, int r){
        if(l==r)
            return lists[l];
        if(l>r)
            return nullptr;
        int mid = l + (r - l)/2;
        return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
    }
    ListNode* mergeTwoLists(ListNode* a,ListNode *b){
        if(!a||!b)
            return a?a:b;
        ListNode* hair = new ListNode();
        if(a->val<b->val){
            hair->next = a;
            a = a->next;
        }else{
            hair->next = b;
            b = b->next;
        }
        ListNode* cur = hair->next;
        while(a&&b){
            if(a->val<b->val){
                cur->next = a;
                a = a->next;
            }else{
                cur->next = b;
                b = b->next;
            }
            cur = cur->next;
        }
        cur->next = a==nullptr?b:a;
        return hair->next;
    }
};

• 时间复杂度 O(kn*logk)：k为链表个数

• 空间复杂度 O(logk)

  方法三：使用优先队列合并（好）

  这个方法和前两种方法的思路有所不同，我们需要维护当前每个链表没有被合并的元素的最前面一个，k 个链表就最多有 k 个满足这样条件的元素，每次在这些元素里面选取 val 属性最小的元素合并到答案中。在选取最小元素的时候，我们可以用优先队列来优化这个过程。

  class Solution {
  public:
    struct Status {
        int val;
        ListNode *ptr;
        // 重载<操作符。可以对两个Status使用<操作符进行比较
        // C++优先队列默认最大先出，struct的目的就是把最大修改成最小，并无不对。
        bool operator < (const Status &rhs) const {
            return val > rhs.val;
        }
    };
    priority_queue <Status> q;
    // 点号（.）：左边必须为实体。
    // 箭头（->）：左边必须为指针。
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        // 遍历lists
        for (auto node: lists) {
            if (node) q.push({node->val, node});
        }
        ListNode head, *tail = &head;
        while (!q.empty()) {
            auto f = q.top(); q.pop();
            tail->next = f.ptr; 
            tail = tail->next;
            if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
        }
        return head.next;
    }
  };

• 时间复杂度 O(kn*logk)：k为链表个数

• 空间复杂度 O(k)

  方法五：逐一比较

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int len = lists.size();
        vector<ListNode*> heads;
        for(int i=0;i<len;i++)
            heads.push_back(lists[i]);
        ListNode* hair = new ListNode(-1);
        ListNode* cur = hair;
        bool isExit = false;
        int minPos = 0;
        while(1){
            isExit = false;
            for(int i=0;i<len;i++){
                if(heads[i]!=nullptr){
                    if(!isExit){
                        isExit = true;
                        minPos = i;
                    }
                    if(heads[i]->val<heads[minPos]->val){
                        minPos = i;
                    }
                }
            }
            if(!isExit){
                cur->next = nullptr;
                break;
            }
            cur->next = heads[minPos];
            cur = cur->next;
            heads[minPos] = heads[minPos]->next;
        }
        return hair->next;
    }
};

• 时间复杂度 O(kn)：k为链表个数，一共n个节点
• 空间复杂度 O(k)