题目

题目来源：力扣（LeetCode）

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。

示例 1: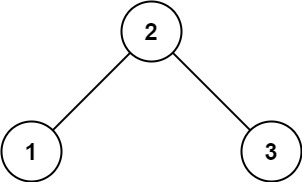
image.png

输入: root = [2,1,3]
输出: 1

示例 2: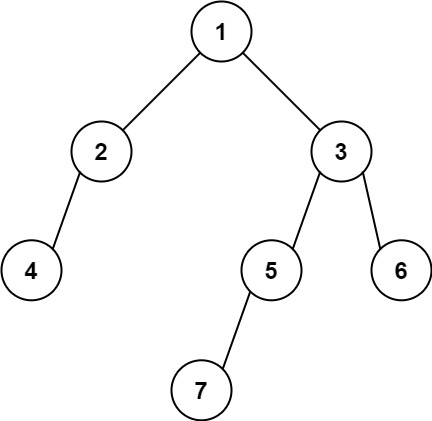
image.png

输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

思路分析

前序遍历 + 回溯 (递归)

  1. 我们使用前序遍历，优先进行左边搜索，判断当前是否是最大深度，当前结点是否是最左边的结点。
  2. 我们可以设置2个全局变量，maxLevel用来记录最大深度，curLevel用来记录当前深度。当结点是叶子结点，且其所 深度比已记录的最大深度大时，我们就更新最左值和最大深度值。
  3. 同深度下只会进行一次值的更新，由于是前序遍历，这唯一一次更新的最左值就是此深度下最左边的 值。
  4. 这样递归完成后，我们就已经找到这颗树最左下角的值了。
  5. 在找最大深度的时候，递归的过程中依然要使用回溯。
  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} root
  11.  * @return {number}
  12.  */
  13. var permute = function (nums) {
  14.   // 保存结果数组(保存每个路径(排列))
  15.   const result = [];
  16.   // 执行回溯函数
  17.   backtrack(nums, []);
  18.   return result;
  20.   // 定义回溯递归函数
  21.   // track 用来存储路径，定义为一个栈
  22.   function backtrack(nums, track) {
  23.     // 递归出口
  24.     // 当收集元素的数组track的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点，将路径推入结果数组，并返回
  25.     if (track.length === nums.length) {
  26.       result.push(track);
  27.       return;
  28.     }
  30.     // 遍历候选字符
  31.     for (let i = 0; i < nums.length; i++) {
  32.       // 如果当前字符在路径中已经被使用过了，则跳过当前字符，进入下一轮循环
  33.       if (track.includes(nums[i])) { continue }
  34.       // 这里说明这个数还没有被使用，入栈 track
  35.       track.push(nums[i]);
  36.       const newTrack = [...track];
  37.       // 继续递归填下一个数
  38.       backtrack(nums, newTrack);
  40.       // 回溯【状态重置】撤销之前的操作
  41.       track.pop();
  42.     }
  43.   }
  44. }
  48. /**
  49.  * @param {number[]} nums
  50.  * @return {number[][]}
  51.  */
  52. var permute = function (nums) {
  53.   // 保存结果数组，保存每个路径（排列）
  54.   const result = []
  55.   // 调用回溯函数，传入参数
  56.   backtracking(nums, nums.length, [], [])
  57.   // 返回结果数组
  58.   return result
  61.   // 定义回溯递归函数，传入数组，长度，节点是否被使用过的数组
  62.   // used 用来标记节点是否被用过 path 用来存储路径，定义为一个栈
  63.   function backtracking(nums, len, used, path) {
  64.     // 递归出口
  65.     // 如果到达叶子节点，将路径推入结果数组，并返回
  66.     if (path.length === len) {
  67.       result.push([...path])
  68.       return
  69.     }
  70.     // 遍历候选字符
  71.     for (let i = 0; i < len; i++) {
  72.       // 使用过就下一轮循环
  73.       if (!used[i]) {
  74.         // undefind和fasle都会进来
  75.         // 这里说明这个数还没有被使用，入栈path
  76.         path.push(nums[i])
  77.         // 标记这个数被使用过了
  78.         used[i] = true
  79.         // 开始进行递归
  80.         backtracking(nums, len, used, path)
  81.         // 回溯【状态重置】撤销之前的操作
  82.         path.pop()
  83.         used[i] = false
  84.       }
  85.     }
  86.   }
  87. };
  91. var findBottomLeftValue = function (root) {
  92.   // 记录最大深度，初值设置为负无穷，方便比较
  93.   let maxLevel = -Infinity,
  94.     // 当前深度
  95.     curLevel = 0,
  96.     // 最左值
  97.     maxLeftVal = 0
  98.   // 前序遍历
  99.   let preOrderTraversal = function (node) {
  100.     // 如果结点不存在则返回
  101.     if (!node) return
  102.     // 当前深度递增
  103.     curLevel++
  104.     // 当结点是叶子结点，且当前深度最大时，它便是树最左下角的结点。
  105.     // 前序遍历优先搜索左边的值，同深度下，最左边的结点最先被搜索到
  106.     // 同深度下，此判断语句内的代码只会被执行一次
  107.     if (curLevel > maxLevel && !node.left && !node.right) {
  108.       // 记录最大深度
  109.       maxLevel = curLevel
  110.       // 记录最左值
  111.       maxLeftVal = node.val
  112.     }
  113.     // 遍历左子树
  114.     node.left && preOrderTraversal(node.left)
  115.     // 遍历右子树
  116.     node.right && preOrderTraversal(node.right)
  117.     // 回溯，深度递减
  118.     curLevel--
  119.   }
  120.   // 从根结点开始向下遍历
  121.   preOrderTraversal(root)
  122.   return maxLeftVal
  123. };