题目

题目来源：力扣（LeetCode

给定一个有 N 个结点的二叉树的根结点 root，树中的每个结点上都对应有 node.val 枚硬币，并且总共有 N 枚硬币。
在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点，或者从子结点移动到父结点。)。

返回使每个结点上只有一枚硬币所需的移动次数。

示例 1：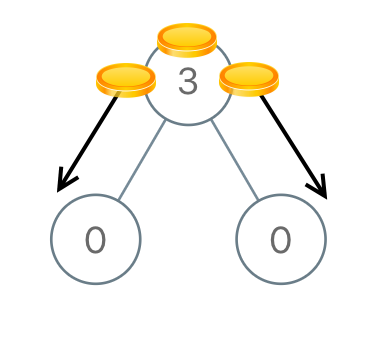
image.png
输入：[3,0,0]
输出：2
解释：从树的根结点开始，我们将一枚硬币移到它的左子结点上，一枚硬币移到它的右子结点上。

示例 2：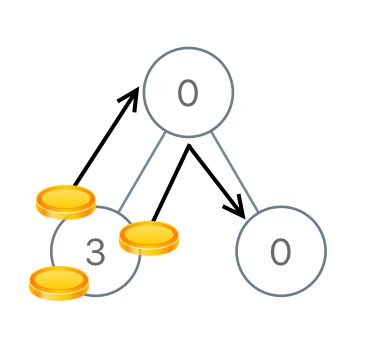
image.png
输入：[0,3,0]
输出：3
解释：从根结点的左子结点开始，我们将两枚硬币移到根结点上 [移动两次]。然后，我们把一枚硬币从根结点移到右子结点上。

示例 3：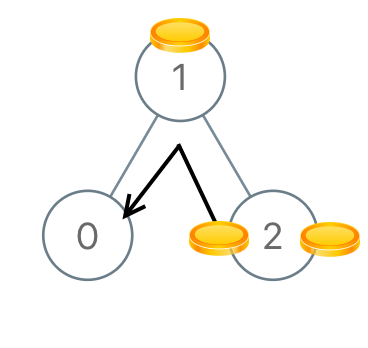
image.png
输入：[1,0,2]
输出：2

示例 4：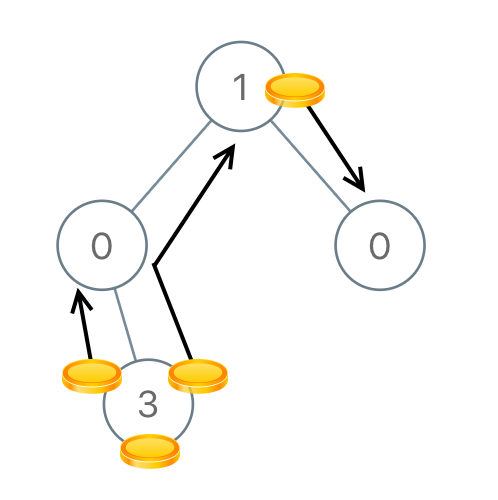
image.png
输入：[1,0,0,null,3]
输出：4

思路分析

根据官方题解，画个图便于理解：

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} root
  11.  * @return {number}
  12.  */
  14. // 如果树的叶子仅包含 0 枚金币（与它所需相比，它的 过载量 为 -1），那么我们需要从它的父亲节点移动一枚金币到这个叶子节点上。
  15. // 如果说，一个叶子节点包含 4 枚金币（它的 过载量 为 3），那么我们需要将这个叶子节点中的 3 枚金币移动到别的地方去。
  16. // 总的来说，对于一个叶子节点，需要移动到它中或需要从它移动到它的父亲中的金币数量为 过载量 = Math.abs(num_coins - 1)
  18. var distributeCoins = function(root) {
  19.   let ans = 0;
  20.   dfs(root);
  21.   return ans;
  22.   // 定义 dfs(node) 为这个节点所在的子树中金币的 过载量，也就是这个子树中金币的数量减去这个子树中节点的数量
  23.   function dfs(node) {
  24.     if (node == null) return 0;
  25.     // 左子树的过载量
  26.     const L = dfs(node.left);
  27.     // 右子树的过载量
  28.     const R = dfs(node.right);
  29.     // 子节点的移动总次数
  30.     ans += Math.abs(L) + Math.abs(R);
  31.     // node.val + L + R - 1 表示当前节点的过载量：当前节点的val + 左右子树的过载量 - 1 (减 1 是因为这个节点只能有一个硬币)
  32.     return node.val + L + R - 1
  33.   }
  34. };