等差数列划分

题目

题目来源：力扣（LeetCode）

如果一个数列 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该数列为等差数列。

例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
给你一个整数数组 nums ，返回数组 nums 中所有为等差数组的 子数组 个数。

子数组 是数组中的一个连续序列。

示例 1：

输入：nums = [1,2,3,4]
输出：3
解释：nums 中有三个子等差数组：[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。

示例 2：

输入：nums = [1]
输出：0

思路分析

动态规划

根据题意，数组nums的长度小于3的时候是不能构成等差数列的。因此如果数组长度小于3，我们可以直接返回0。

1、状态定义
dp[i]：表示以 nums[i] 结尾的、且长度大于等于 3 的连续等差数列的个数

2、状态转移方程
如果 nums[i] 能够接在 nums[i - 1] 的后面形成一个更长的 (在原数组上连续的) 等差数列，那么 dp[i] = dp[i - 1] + 1 。我们通过一个图来理解这段话：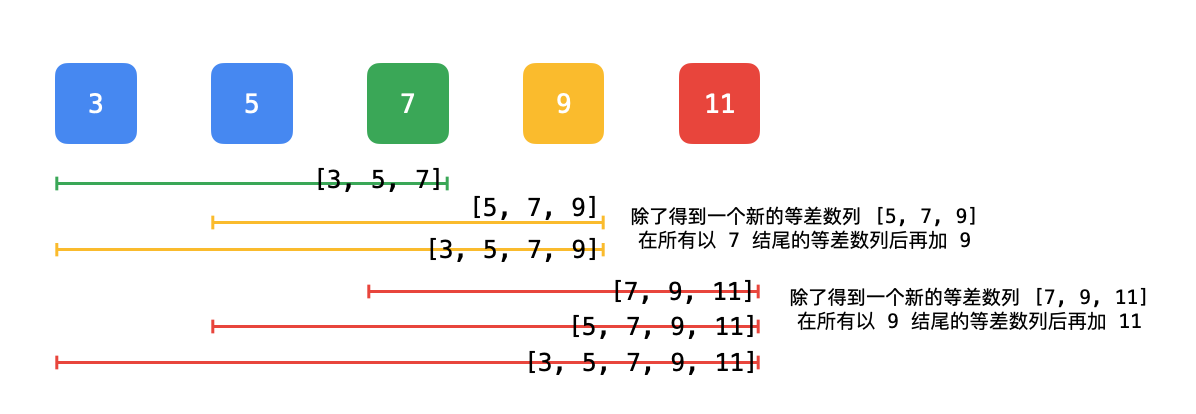

代码实现

/**
 * @param {number[]} nums
 * @return {number}
 */
var numberOfArithmeticSlices = function (nums) {
  if (nums.length < 3) return 0
  const dp = new Array(nums.length).fill(0)
  // 统计等差数列的数量
  let sum = 0
  for (let i = 1; i < nums.length - 1; i++) {
    // 隐含了判断等差数列的长度大于等于 3
    if (nums[i] - nums[i - 1] === nums[i + 1] - nums[i]) {
      dp[i + 1] = dp[i] + 1
      sum += dp[i + 1]
    }
  }
  return sum
};