动态规划 - 摆动序列 - 《数据结构与算法》

题目
思路分析

题目

题目来源：力扣（LeetCode）

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个摆动序列，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为摆动序列的最长子序列的长度。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

思路分析

写在前面

某个序列被称为「上升摆动序列」，当且仅当该序列是摆动序列，且最后两个元素呈上升趋势。如序列 [1,3,2,4][1,3,2,4] 即为「上升摆动序列」。
某个序列被称为「下降摆动序列」，当且仅当该序列是摆动序列，且最后两个元素呈下降趋势。如序列 [4,2,3,1][4,2,3,1] 即为「下降摆动序列」。
特别地，对于长度为 1 的序列，它既是「上升摆动序列」，也是「下降摆动序列」

动态规划

1、状态定义

up[i] 表示以 nums 的前 i 个元素中的某一个元素为结尾的最长的「上升摆动序列」的长度。
down[i] 表示以 nums 的前 i 个元素中的某一个元素为结尾的最长的「下降摆动序列」的长度。

2、状态转移公式

当 nums[i] < nums[i - 1] 时，即当前元素小于前一个元素，根据摆动序列的定义，当前元素应该在「下降摆动序列」中，down[i] 既可以从 down[i - 1] 转移，也可以从 up[i - 1] 转移
- 从down[i - 1] 中转移，我们可以废弃掉「下降摆动序列」的最后一个元素，然后将当前元素添加到「下降摆动序列」中，也可以不做处理，那么 down[i] = down[i - 1]
- 从up[i - 1] 中转移，将当前元素放入「上升摆动序列」中，令其成为新的 down，即 down[i] = up[i - 1] + 1
- 此时「上升摆动序列」保持不变 up[i] = up[i - 1]
当 nums[i] > nums[i -1 ] 时，即当前元素大于前一个元素，根据摆动序列的定义，当前元素应该在「上升摆动序列」中，此时 up[i] 既可以从 up[i - 1] 转移，也可以从 down[i - 1] 转移
- 从 up[i - 1] 转移，我们可以废弃掉「上升摆动序列」中的最后一个元素，然后将当前元素添加到「上升摆动序列」中，也可不做处理，那么 up[i] = up[i - 1]
- 从 down[i - 1] 转移，将当前元素放入「下降摆动序列」中，令其成为新的，即 up[i] = down[i - 1] + 1
- 此时「下降摆动序列」保持不变 down[i] = down[i - 1]
当 nums[i] == nums[i - 1] 时，当前元素不能用于任何序列，「上升摆动序列」和「下降摆动序列」保持不变

因此，最终的状态转移方程为：

up[i] = up[i - 1] (nums[i] ≤ nums[i - 1])
up[i] = max(up[i - 1], down[i - 1] + 1) (nums[i] > nums[i - 1])

down[i] = down[i - 1] (nums[i] ≥ nums[i - 1])
down[i] = max(up[i - 1] + 1, down[i - 1]) (nums[i] < nums[i - 1])

3、状态初始化
开始时，遍历到 nums 数组中的第一个元素，因为此时只遍历了一个元素，所以，「上升摆动序列」和「下降摆动序列」的长度为 1。

4、返回值
up[n - 1] 和 down[n - 1] 中的较大值即为最后的答案，其中 n 是序列的长度。

5、举例说明
以 nums=[1,7,4,9,2,5] 为例，演示如下：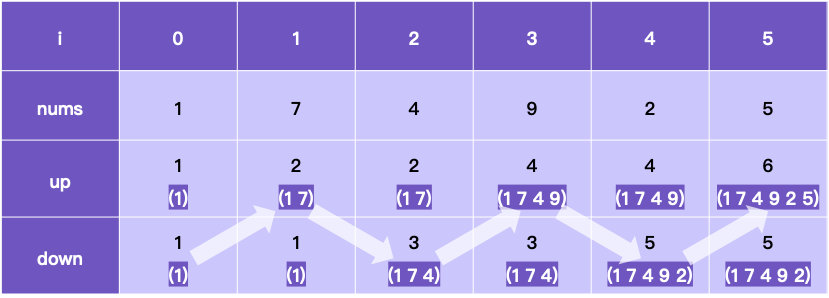

代码实现

/**
 * @param {number[]} nums
 * @return {number}
 */
var wiggleMaxLength = function (nums) {
  const n = nums.length;
  // nums中元素少于两个，即 nums 只有 0 个或 1 个元素摆动序列长度对应为 0 或 1
  if (n < 2) return n;
  // 上升摆动序列
  const up = new Array(n).fill(0);
  // 下降摆动序列
  const down = new Array(n).fill(0);
  // 开始时，取 nums 数组中的第一个元素，因此「上升摆动序列」和「下降摆动序列」的长度为 1
  up[0] = down[0] = 1;
  for (let i = 1; i < n; i++) {
    // nums[i] > nums[i - 1]，当前元素应该在「上升摆动序列」中
    if (nums[i] > nums[i - 1]) {
      up[i] = Math.max(up[i - 1], down[i - 1] + 1);
      down[i] = down[i - 1];
    } 
    // nums[i] < nums[i - 1]，当前元素应该在 「下降摆动序列」中
    else if (nums[i] < nums[i - 1]) {
      up[i] = up[i - 1];
      down[i] = Math.max(up[i - 1] + 1, down[i - 1]);
    } else {
      // nums[i] == nums[i - 1] 时，当前元素不能用于任何序列，「上升摆动序列」和「下降摆动序列」保持不变
      up[i] = up[i - 1];
      down[i] = down[i - 1];
    }
  }
  // up[n - 1] 和 down[n - 1] 中的较大值即为最后的答案
  return Math.max(up[n - 1], down[n - 1]);
};

空间优化
注意到 down 和 up 只和前一个状态有关，所以我们可以优化存储，分别用一个变量维护即可。

/**
 * @param {number[]} nums
 * @return {number}
 */
var wiggleMaxLength = function (nums) {
  const n = nums.length;
  // nums中元素少于两个，即 nums 只有 0 个或 1 个元素摆动序列长度对应为 0 或 1
  if (n < 2) {
    return n;
  }
  // 开始时，取 nums 数组中的第一个元素，因此「上升摆动序列」和「下降摆动序列」的长度为 1
  let up = down = 1;
  for (let i = 1; i < n; i++) {
    // nums[i] > nums[i - 1]，当前元素应该在「上升摆动序列」中
    if (nums[i] > nums[i - 1]) {
      up = Math.max(up, down + 1);
    }
    // nums[i] < nums[i - 1]，当前元素应该在 「下降摆动序列」中
    else if (nums[i] < nums[i - 1]) {
      down = Math.max(up + 1, down);
    }
  }
  /// up 和 down 中的较大值即为最后的答案
  return Math.max(up, down);
};

参考阅读 https://leetcode-cn.com/problems/wiggle-subsequence/solution/bai-dong-xu-lie-by-leetcode-solution-yh2m/ https://leetcode-cn.com/problems/wiggle-subsequence/solution/tan-xin-si-lu-qing-xi-er-zheng-que-de-ti-jie-by-lg/ https://leetcode-cn.com/problems/wiggle-subsequence/solution/dong-tai-gui-hua-tan-xin-suan-fa-1xing-d-ig8l/