题目

题目来源：力扣（LeetCode）

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

思路分析

贪心策略

我们看看下面这个跳跃数组的特点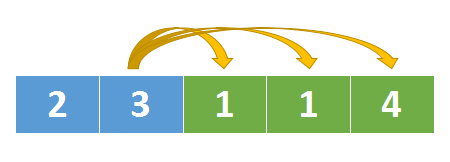
image.png
从nums[1]也就是3 可以跳跃到最后一个位置，因为它可以跳一步，跳两步，跳三步。
即以nums[1]为起点，后面三格位置都是可达的，也就是如果某个数组下标i是可达的，那么i+1，i+2，i+3。。。i+nums[i]这片区域都是可达的。

于是我们只需要维护一个最远可达的下标，然后遍历整个数组，如果数组遍历完后，这个最远可达的下标是大于等于 数组最后一个位置，那么说明最后一个位置是可达的，否则最后一个位置不可达。
如果还是不清楚的话看下面这个图应该就能明白了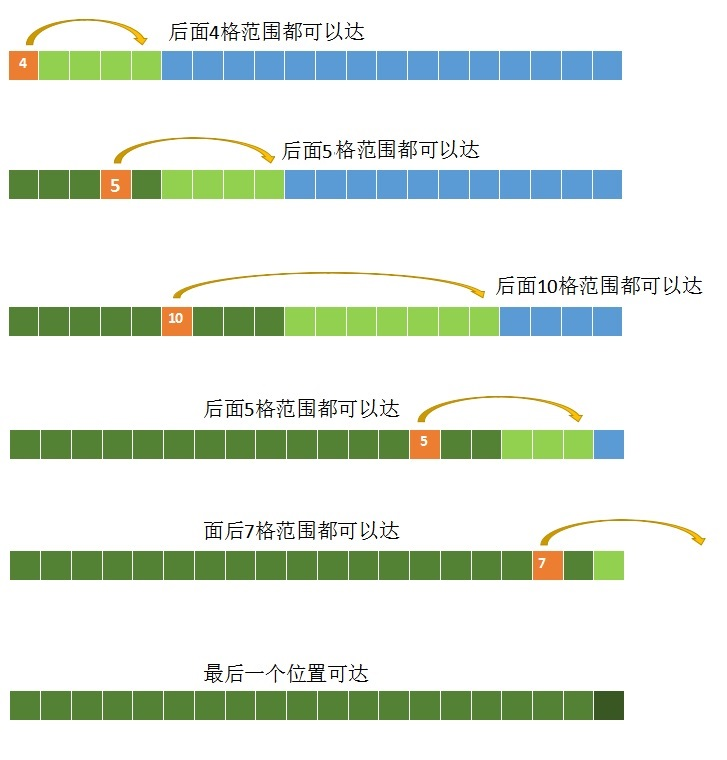
image.png
上图中浅绿色表示可以扩大的可达范围，深绿色部分表示已知的可达范围。我们在遍历的时候，不断尝试是否可以扩大可达范围，也就是图中的浅绿色部分，一旦可达那么这片区域就变成深绿色的了。
我们不用等到深绿色最右边再判断，比如对于第三排橙色格子10，它没有达到深绿色最右边，但是它所在的位置，可以扩大 绿色边界。
当整个遍历结束后，我们记录的最大可达范围是大于数组最后一个位置，所以这个数组最后一位是可达的，返回true。

再看一个不可达的例子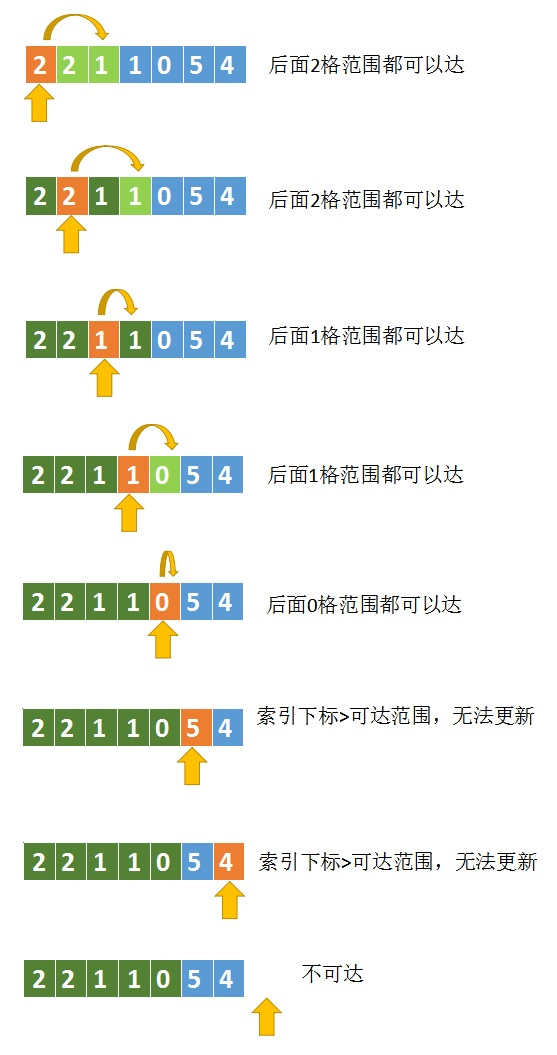
image.png
看完这个图，应该就很明确了，每次更新的时候，看看最大可达范围是否 大于等于当前遍历到的数组下标，如果是才更新。否则说明这个区域是不可达的，当然也就不用更新了。
通过上面的图也可以发现，还有一个优化点，如果当前遍历到的下标比最大可达范围大，可以直接跳出判断了。

  1. /**
  2.  * @param {number[]} nums
  3.  * @return {boolean}
  4.  */
  5. var canJump = function (nums) {
  6.   // 如果是起点即终点，直接返回true。
  7.   if (nums == null || nums.length == 0) {
  8.     return true;
  9.   }
  10.   let n = nums.length;
  11.   // 记录当前能到达最远的元素下标
  12.   let maxPosition = 0;
  13.   //遍历数组，尝试扩大最大可达范围
  14.   for (let i = 0; i < n; ++i) {
  15.     if (maxPosition >= i) {
  16.       // maxPosition 取能到达的最远的下标
  17.       maxPosition = Math.max(maxPosition, i + nums[i]);
  18.     }
  19.   }
  20.   // 如果能够到达最后一个下标或者跳过头了，说明可以到达。
  21.   if (maxPosition >= n - 1) {
  22.     return true;
  23.   }
  24.   // 如果 maxPosition 已经是当前的下标了，并且当前不能再往前走了，肯定是到达不了终点了。
  25.   return false;
  27. };

参考阅读 https://leetcode-cn.com/problems/jump-game/solution/chao-xiang-xi-tu-jie-di-gui-tan-xin-55-tiao-yue-yo/