打乱数组

题目

题目来源：力扣（LeetCode）

给你一个整数数组 nums ，设计算法来打乱一个没有重复元素的数组。

实现 Solution class:

Solution(int[] nums) 使用整数数组 nums 初始化对象
int[] reset() 重设数组到它的初始状态并返回
int[] shuffle() 返回数组随机打乱后的结果

示例：

输入
[“Solution”, “shuffle”, “reset”, “shuffle”]
[[[1, 2, 3]], [], [], []]
输出
[null, [3, 1, 2], [1, 2, 3], [1, 3, 2]]

解释
Solution solution = new Solution([1, 2, 3]);
solution.shuffle(); // 打乱数组 [1,2,3] 并返回结果。任何 [1,2,3]的排列返回的概率应该相同。例如，返回 [3, 1, 2]
solution.reset(); // 重设数组到它的初始状态 [1, 2, 3] 。返回 [1, 2, 3]
solution.shuffle(); // 随机返回数组 [1, 2, 3] 打乱后的结果。例如，返回 [1, 3, 2]

思路分析

Fisher-Yates 洗牌算法

Fisher–Yates随机置乱算法也被称做高纳德置乱算法，通俗说就是生成一个有限集合的随机排列。
Fisher-Yates随机置乱算法是无偏的，所以每个排列都是等可能的，当前使用的Fisher-Yates随机置乱算法是相当有效的，需要的时间正比于要随机置乱的数，不需要额为的存储空间开销。

洗牌算法，将原数组打散，使原数组的某个数在打散后的数组中的每个位置等概率出现，评判标准是n个数字必须有n!种可能

洗牌算法的四种形式

// 获取闭区间 [n, m] 内的一个随机整数
function randOne(n, m) {
  return Math.floor(Math.random() * (m - n + 1)) + n;
};
// 第一种写法
function shuffle(arr) {
    const n = arr.length();
    /******** 区别只有这两行 ********/
    for (let i = 0 ; i < n; i++) {
        // 从 i 到最后随机选一个元素
        const rand = randOne(i, n - 1);
    /**********************8888***/
        // 交换 arr 数组i和rand下标的两个元素
        [ arr[i], arr[rand] ] = [ arr[rand], arr[i] ];
    }
}
// 第二种写法
    for (let i = 0 ; i < n - 1; i++)
        const rand = randOne(i, n - 1);
// 第三种写法
    for (let i = n - 1 ; i >= 0; i--)
        const rand = randOne(0, i);
// 第四种写法
    for (let i = n - 1 ; i > 0; i--)
        const rand = randOne(0, i);

第二种写法，与第一种写法的迭代都是一样的，只是少了一次迭代而已。第三种写法就是第一种写法，只是将数组从后往前迭代而已；第四种写法是第二种写法从后往前来。

n个数产生的结果必须有n!种可能。遍历nums数组，每次取[i, n-1]闭区间的一个随机数nums[rand]， 交换nums[i]和nums[rand]即可；

假设传入这样的一个数组：nums = [1, 2, 3, 4, 5]，执行 for循环如下：

for 循环第一轮迭代时，i = 0，rand 的取值范围是 [0, 4]，有 5 个可能的取值，假设 randOne(0, 4) 为 3，则交换 nums[0] 和 nums[3] ，如下图：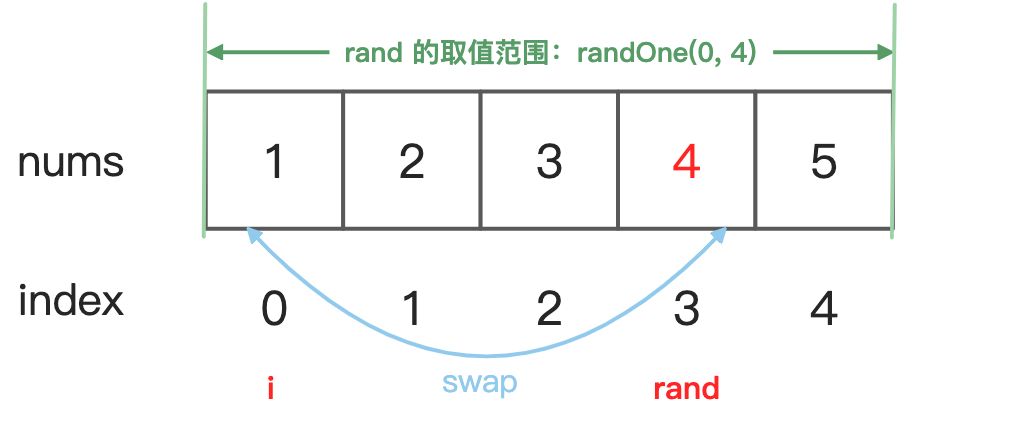

for 循环第二轮迭代时，i = 1，rand 的取值范围是 [1, 4]，有 4 个可能的取值，假设 randOne(1, 4) 的值为 4，则交换 nums[1] 和 nums[4]，如下图：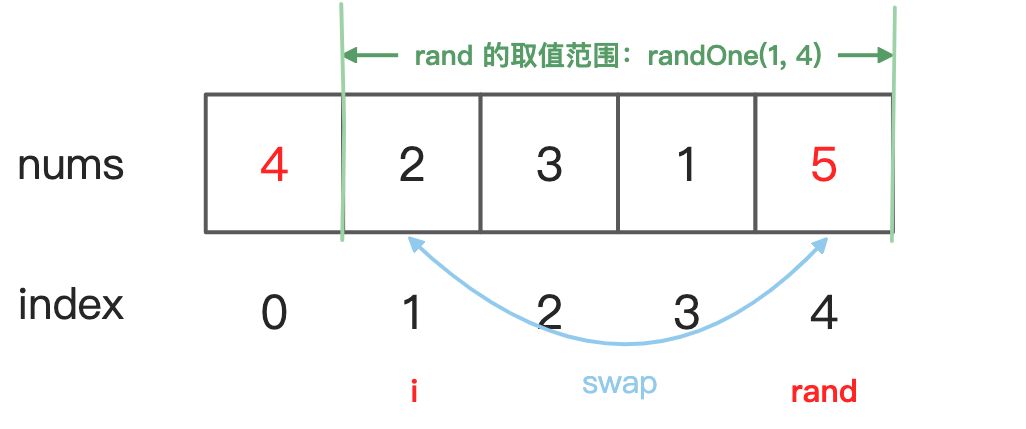

后面以此类推，直到最后一次迭代，i = 4，rand 的取值范围是 [4, 4]，只有 1 个可能的取值，如下图：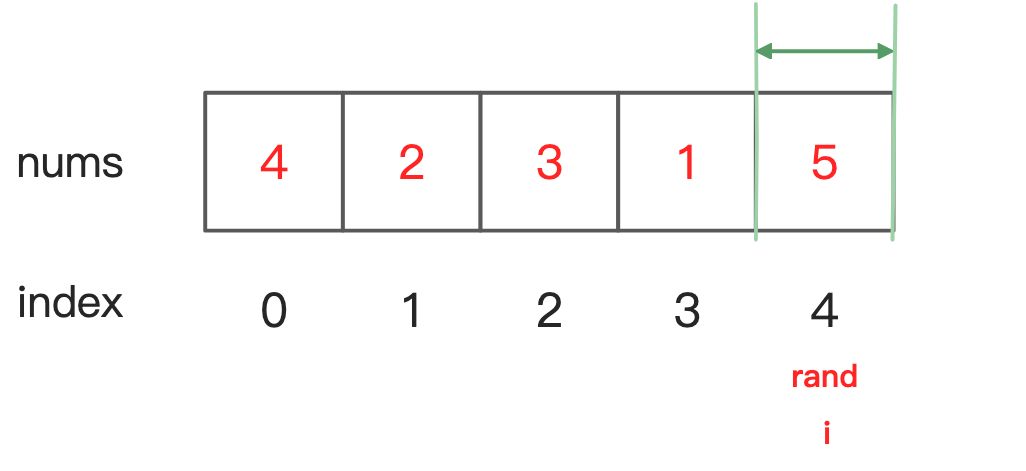

整个过程产生的所有可能结果有 n! = 5! = 54321 = 120 种。

/**
 * @param {number[]} nums
 */
var Solution = function(nums) {
  this.nums = nums;
};
/**
 * Resets the array to its original configuration and return it.
 * @return {number[]}
 */
Solution.prototype.reset = function() {
  return this.nums;
};
/**
 * Returns a random shuffling of the array.
 * @return {number[]}
 */
Solution.prototype.shuffle = function() {
  const nums = this.nums.slice(0);
  const n = nums.length;
  for (let i = 0; i < n; i++) {
    const rand = randOne(i, n - 1);
    [nums[i], nums[rand]] = [nums[rand], nums[i]]
  }
  return nums;
};
function randOne(n, m) {
  return Math.floor(Math.random() * (m - n + 1)) + n;
}
/**
 * Your Solution object will be instantiated and called as such:
 * var obj = new Solution(nums)
 * var param_1 = obj.reset()
 * var param_2 = obj.shuffle()
 */

拓展阅读：https://www.cnblogs.com/labuladong/p/12320471.html