二叉树 - 117. 填充每个节点的下一个右侧节点指针 II - 《数据结构与算法》

题目

题目

题目来源：力扣（LeetCode）

给定一个二叉树

struct Node {
int val;
Node left;
Node right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：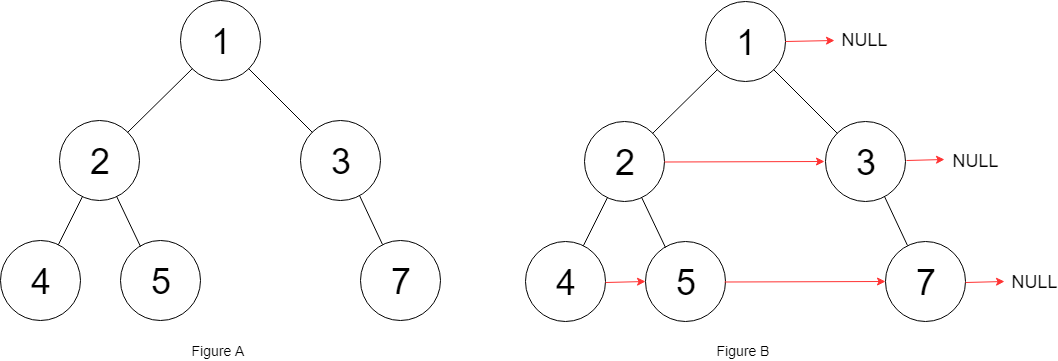

输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），’#’ 表示每层的末尾。

广度优先搜索

在树中，广度优先搜索按照层的顺序遍历二叉树，在遍历第 i 层前，一定会先遍历完第 i - 1 层。

我们可以设计如下的算法：初始化一个队列 queue，首先将根节点放入队列中。当队列不为空的时候，记录当前队列大小为 size，从队列中取出这 size 个节点并通过这 size 个元素拓展下一层新节点。如此循环，直到队列为空。

这样可以保证每次遍历的 size 个节点都是同一层的。我们在遍历每一层的时候修改这一层节点的 next 指针，将每一层连接成一个链表。

代码

/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */
/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function (root) {
  if (root === null) {
    return null;
  }
  const queue = [root];
  while (queue.length) {
    // 每一层的节点数量
    const size = queue.length;
    let last = null;
    for (let i = 1; i <= size; ++i) {
      // 出队
      let f = queue.shift();
      // 左子节点如果不为空，则加入队列
      if (f.left !== null) {
        queue.push(f.left);
      }
      // 右子节点如果不为空，则加入队列
      if (f.right !== null) {
        queue.push(f.right);
      }
      // 当前遍历的节点不是这一层的第一个节点，则用前一个节点的 next 指针指向它
      if (i !== 1) {
        last.next = f;
      }
      last = f;
    }
  }
  return root;
};

使用 next 指针

在「广度优先搜索」方法中，由于使用了队列来辅助遍历树，因此需要队列的额外空间。我们也可以不使用队列，通过 next 指针去访问每一层的所有节点，从而节省空间。

具体做法是：

从根节点开始。因为第 0 层只有一个节点，不需要处理。可以在上一层为下一层建立 next 指针。该方法最重要的一点是：位于第 x 层时为第 x + 1 层建立 next 指针。一旦完成这些连接操作，移至第 x + 1 层为第 x + 2 层建立 next 指针。
当遍历到某层节点时，该层节点的 next 指针已经建立。这样就不需要队列从而节省空间。每次只要知道下一层的最左边的节点，就可以从该节点开始，像遍历链表一样遍历该层的所有节点。

代码

/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */
/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function (root) {
  if (root == null) return root;
  // 把 cur 看做是每一层的链表
  let cur = root;
  while (cur != null) {
    // 遍历当前层的时候，为了方便操作，在下一层前面添加一个虚拟头结点（注意这里是访问
    // 当前层的节点，然后把下一层的节点串起来）
    let dummy = new Node(-1);
    // pre 表示访问下一层节点的前一个节点
    let pre = dummy;
    // 开始遍历当前层的链表
    while (cur != null) {
      if (cur.left != null) {
        // 如果当前节点的左子节点不为空，就让 pre 的 next 指针指向左子节点，也就是把它串联起来
        pre.next = cur.left;
        // 移动 pre 到当前节点的左子节点上
        pre = pre.next;
      }
      if (cur.right != null) {
        // 如果当前节点的右子节点不为空，就让 pre 的 next 指针指向右子节点，也就是把它串联起来
        pre.next = cur.right;
        // 移动 pre 到当前节点的右子节点上
        pre = pre.next;
      }
      // 继续访问这一行的下一个季度
      cur = cur.next;
    }
    // 把下一层串联成一个链表之后，让他赋值给cur，
    // 然后续继续循环，直到cur为空为止
    cur = dummy.next;
  }
  return root;
};