题目

题目来源：力扣（LeetCode）

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

思路分析

「归并排序」与「逆序对」是息息相关的。归并排序体现了 “分而治之” 的算法思想，具体为：

  • 分： 不断将数组从中点位置划分开（即二分法），将整个数组的排序问题转化为子数组的排序问题；
  • 治： 划分到子数组长度为 1 时，开始向上合并，不断将 较短排序数组 合并为 较长排序数组，直至合并至原数组时完成排序；

如下图所示，为数组 [7, 3, 2, 6, 0, 1, 5, 4][7,3,2,6,0,1,5,4] 的归并排序过程。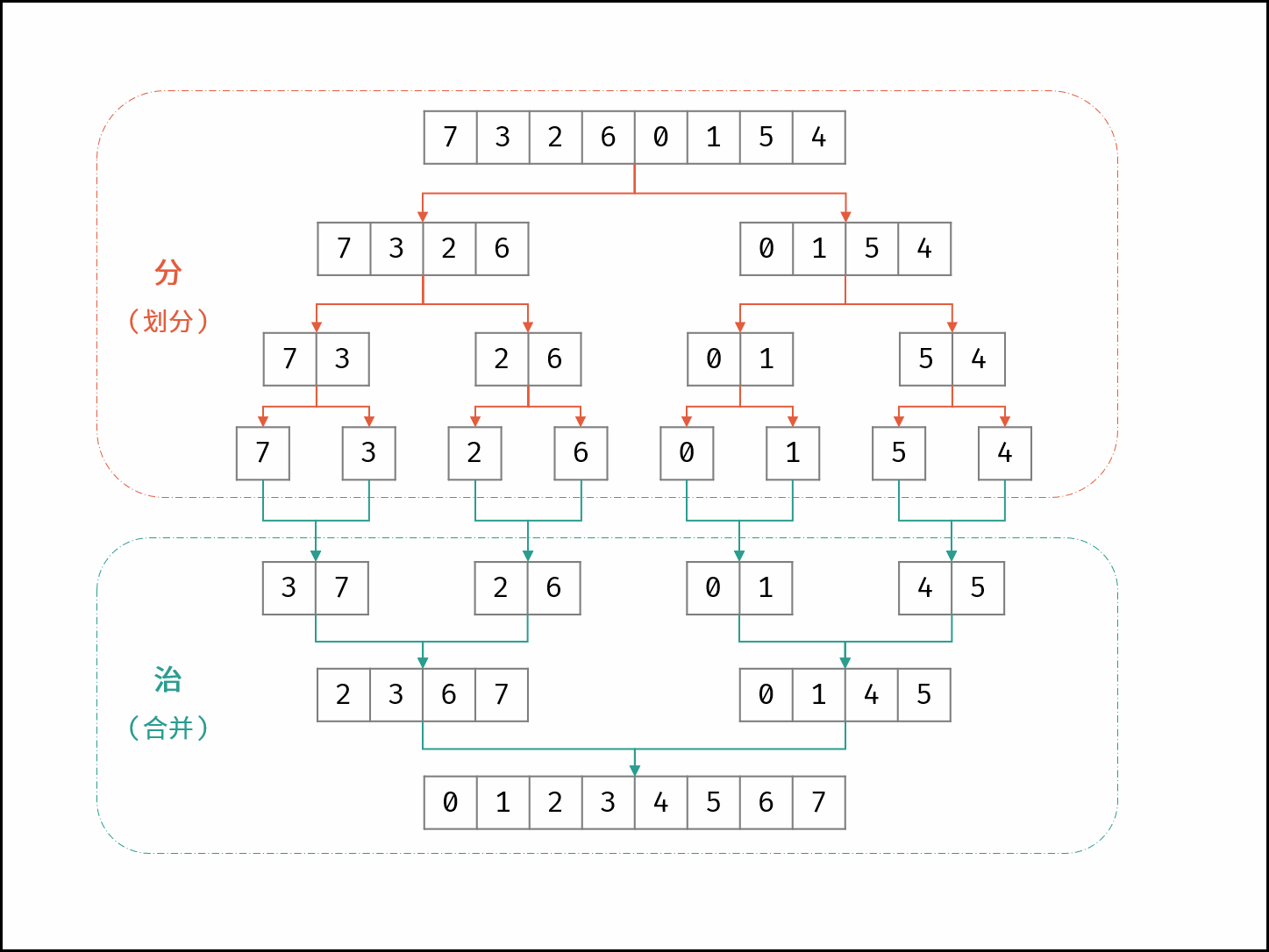
image.png

合并阶段 本质上是 合并两个排序数组 的过程，而每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」 。

如下图所示，为数组 [7, 3, 2, 6, 0, 1, 5, 4][7,3,2,6,0,1,5,4] 的归并排序与逆序对统计过程。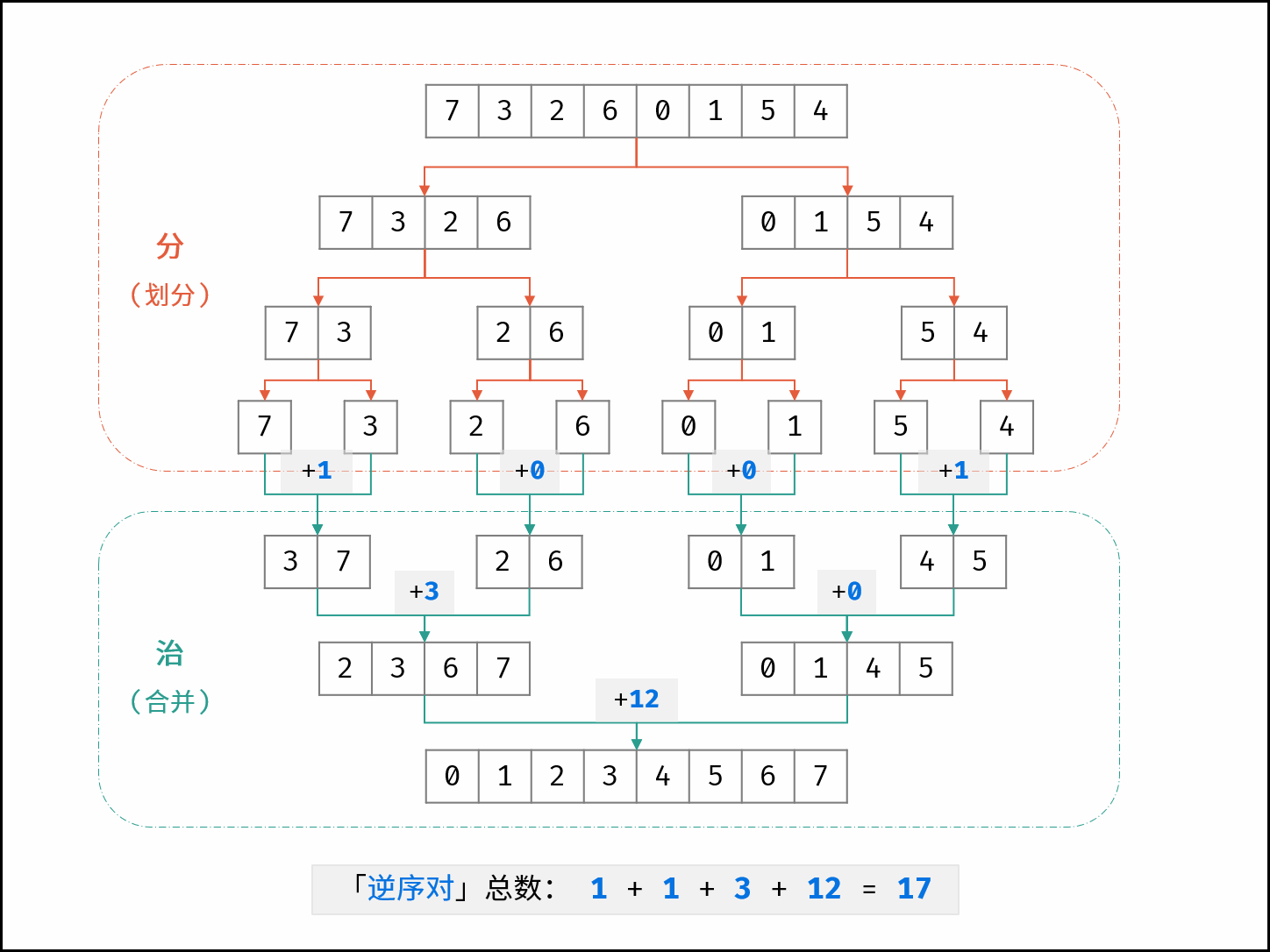
image.png

  1. /**
  2.  * @param {number[]} nums
  3.  * @return {number}
  4.  */
  5. let temp = [];// 因为用到的是归并排序，归并排序得用到一个额外的存储数叫temp
  6. var reversePairs = function (nums) {
  7.   // 把temp的存储大小扩展成和nums的一样大
  8.   while (temp.length < nums.length) temp.push(0);
  9.   // 对应下标
  10.   return countReversePairs(nums, 0, nums.length - 1)// 首尾下标传进去；
  11. };
  12. var countReversePairs = function (nums, leftRoot, rightRoot) {//待排序数组，从l-r的统计区间
  13.   if (leftRoot >= rightRoot) return 0;//空区间/只包含一个元素的区间，的时候，逆序对的个数为0
  14.   let mid = (leftRoot + rightRoot) >> 1;//右移动1位就是除以2；计算中间数的位置
  15.   let ans = 0;
  16.   ans += countReversePairs(nums, leftRoot, mid);//左边逆序对的个数
  17.   ans += countReversePairs(nums, mid + 1, rightRoot);//右边逆序对的个数
  18.   // 加上横跨两边的逆序对的数量
  19.   let k = leftRoot, p1 = leftRoot, p2 = mid + 1;//分别指向左右区间的第一位；
  20.   while ((p1 <= mid) || (p2 <= rightRoot)) { //第一个区间不为空，第二个区间不为空
  21.     if ((p2 > rightRoot) || (p1 <= mid && nums[p1] <= nums[p2])) { //第一个区间的元素放进来
  22.       temp[k++] = nums[p1++];
  23.     } else {
  24.       temp[k++] = nums[p2++];//将第二个区间放进来，这个时候就可以统计逆序对的数量
  25.       ans += (mid - p1 + 1);//左区间剩余的逆序对的数量
  26.     }
  27.   }
  28.   //将temp的元素拷贝到原数组里面，对应下下标，temp是从外面定义的一个全局的元素，nums从l到r，temp也是从l到r,所以这个数组的空间大小是有序的
  29.   for (let i = 0; i <= rightRoot; i++) nums[i] = temp[i];
  30.   return ans;//ans 就是从l -r 的逆序数的数量
  31. }