二叉树 - 翻转二叉树以匹配先序遍历 - 《数据结构与算法》

题目
思路分析

题目

题目来源：力扣（LeetCode）

给你一棵二叉树的根节点 root ，树中有 n 个节点，每个节点都有一个不同于其他节点且处于 1 到 n 之间的值。

另给你一个由 n 个值组成的行程序列 voyage ，表示预期的二叉树先序遍历结果。

通过交换节点的左右子树，可以翻转该二叉树中的任意节点。例，翻转节点 1 的效果如下：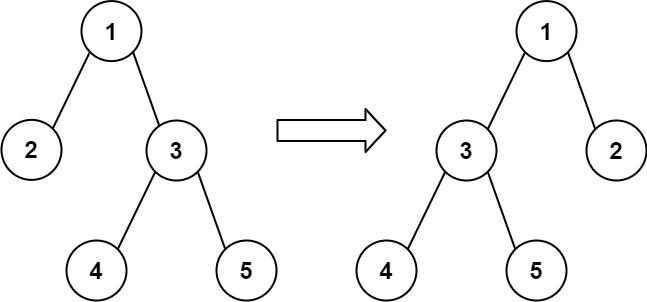

请翻转最少的树中节点，使二叉树的先序遍历与预期的遍历行程 voyage 相匹配。

如果可以，则返回翻转的所有节点的值的列表。你可以按任何顺序返回答案。如果不能，则返回列表 [-1]。

示例 1：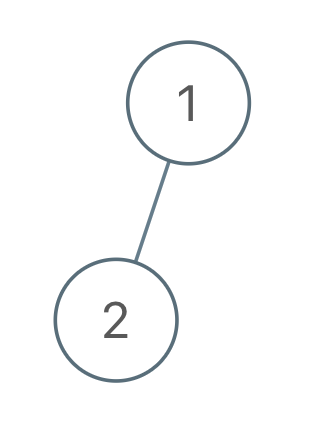

输入：root = [1,2], voyage = [2,1]
输出：[-1]
解释：翻转节点无法令先序遍历匹配预期行程。

示例 2：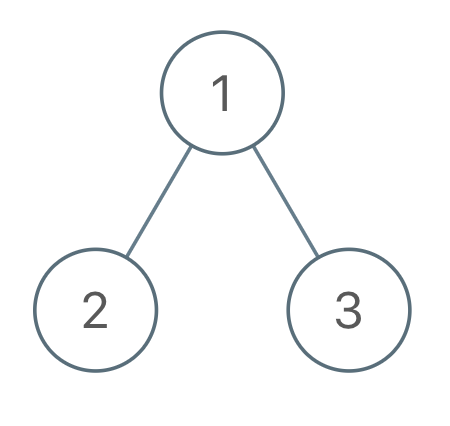

输入：root = [1,2,3], voyage = [1,3,2]
输出：[1]
解释：交换节点 2 和 3 来翻转节点 1 ，先序遍历可以匹配预期行程。

示例 3：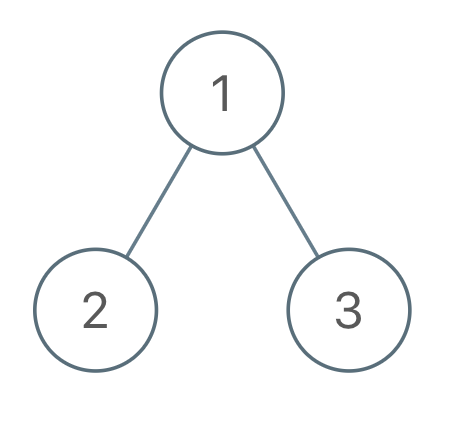

输入：root = [1,2,3], voyage = [1,2,3]
输出：[]
解释：先序遍历已经匹配预期行程，所以不需要翻转节点。

思路分析

题目给出了一个待操作的树 A 的根节点 root，和树 V 先序遍历的结果数组，然后求的是 A 能否翻转最少的 n 个节点，使得 A 和 V 一致。
我们遍历树V先序遍历的结果数组voyage (其实相当于是前序遍历树V)，然后用 V 的值去匹配 A，看看能否进行树的匹配
对于一次遍历，我们首先判断根节点的值是一致，才会进入这一次的遍历中，然后主要是看左右树，对于树 V 来说，用 pos 不断按照先序遍历给出值，而对于 V 来说，你可以用左树匹配，如果匹配成功，则啥事没有，大家是一样的；而如果左树不匹配，用右树先行，然后再走左树，这种情况就需要翻转一下当前的节点，保证树 A 要在前序遍历的情况和 V 匹配；
如果在匹配过程中 A 的左右树都没有匹配成功，则会提前走出 A 的遍历，这个时候 pos 就没有迭代完，也就是树A 的节点数量少于树V 的节点数量，这个时候就是异常，返回 [-1]

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number[]} voyage
 * @return {number[]}
 */
var flipMatchVoyage = function (root, voyage) {
  // 用来在进入 dfs 前对根节点的判断
  // 如果根节点的值不一致，则直接返回-1，不再进入dfs
  if (root.val !== voyage[0]) return [-1] 
  const ret = []
  let pos = 0 // 这是用来获取 voyage 值，也是遍历树 V 的，如果没有走完，证明无法匹配 root
  const dfs = root => {
    // 每一次的遍历 pos 都要跟随着
    pos++
    // 对于每一个节点，都是按照先序遍历的写法
    if (root.left && root.left.val === voyage[pos]) {
      // 如果在这节点左树适配，那就继续走，因为这是先序遍历
      dfs(root.left)
    }
    if (root.right && root.right.val === voyage[pos]) {
      dfs(root.right)
      // 右树完成之后，需要看看现在 pos 所在的值是否可以匹配左树，即是否先走右树再走左树，成立即当前的 root 节点就是需要进行翻转的节点
      if (root.left && root.left.val === voyage[pos]) {
        ret.push(root.val)
        dfs(root.left)
      }
    }
  }
  dfs(root)
  // 代码走到此处，代表树A 已经遍历完了
  // 此时 pos 的值代表的就是树A的节点数量，树A 的节点数量少于 树 V 的节点数量，说明不匹配
  if (pos < voyage.length) {
    return [-1]
  }
  return ret
};