数据结构 - 数据结构与算法学习之队列 - 《数据结构与算法》

队列的定义
- 入队列
- 出队列
基于对象的队列
基于数组的队列
基于链表实现队列
队列的应用

队列的定义

队列是一种遵循先进先出原则的线性表。队列只允许在队列的尾部添加元素，在队列的头部删除元素。新添加的元素必须排在队列的末尾。

在现实生活中，最常见的队列的例子就是排队，例如超市里顾客在排队结账。

在计算机科学中，一个常见的例子就是打印队列。比如说我们需要打印五份文档。我们会打开每个文档，然后点击打印按钮。每个文档都会被发送至打印队列。第一个发送到打印队列的文档会首先被打印，以此类推，直到打印完所有的文档。

入队列

下面这张图展示了队列如何添加新的元素：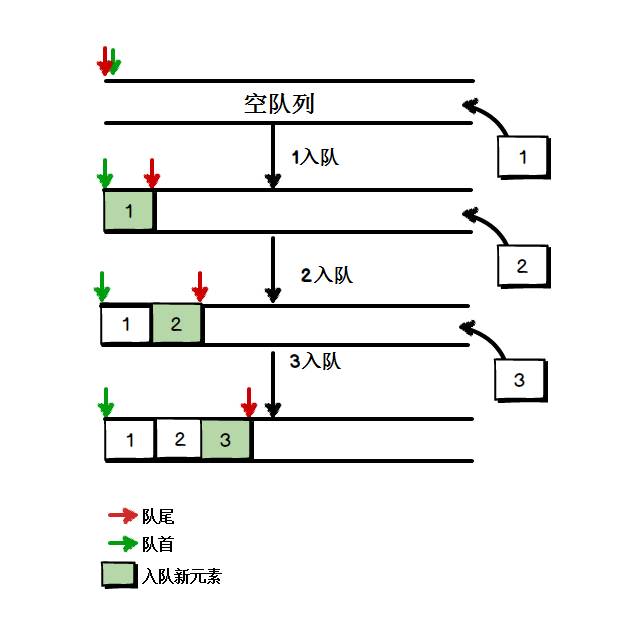

左侧是队列的头部，右侧是队列的尾部，新的元素如果想进入队列，只能从尾部进入。1 从尾部进入队列后，2也只能从尾部进入队列，因此2只能跟在1后面，3只能跟在2后面。

出队列

如果队列中的元素想要出队列，只能从队列的头部出去，如下图：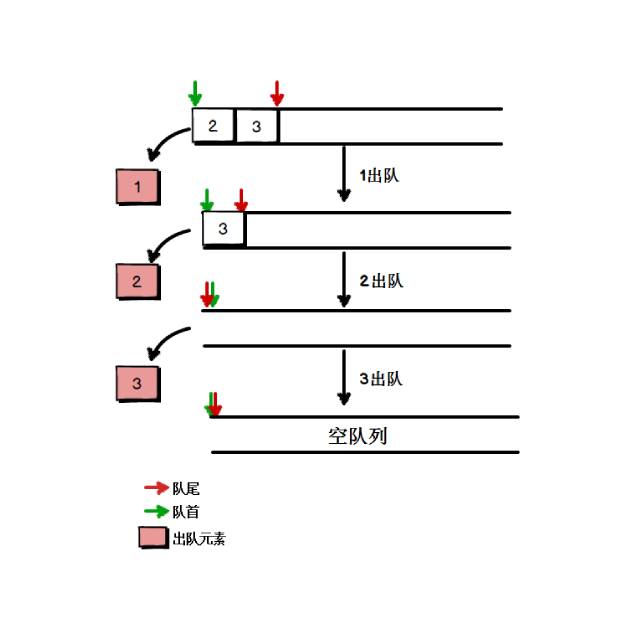
queue (1).jpg
1 首先出队列，接着是2、3，它们出队列的顺序与入队的顺序是一致的。

基于对象的队列

相较于使用数组实现队列，使用Object对象来实现队列，在获取元素时更高效。因此我们使用 ES6 的类来创建一个基于Object 对象的队列：

class Queue {
    constructor() {
      this.count = 0; // 队列的大小
    this.lowestCount = 0; // 追踪队列的头部元素，即头部元素的在对象中的 key
    this.items = {};
  }
}

接下来，为队列声明一些队列可用的方法：

enqueue(element) 向队列尾部添加一个新的元素
dequeue() 移除队列头部的元素
head() 查看队列头部的元素（注意：不是删除，只是查看）
tail() 查看队列尾部元素（注意：不是删除，只是查看）
isEmpty() 判断队列是否为空
clear() 清空队列
size() 返回队列的大小
print() 打印队列

下面，我们逐一实现这些方法：

enqueue 向队列尾部添加元素

enqueue 方法负责向队列尾部添加新元素，注意，只能从尾部添加新元素

// 向队列尾部添加新元素
enqueue(element) {
    this.items[this.count] = element;
  this.count++;
}

dequeue 移除队列头部元素

dequeue 方法负责移除队列头部的元素。由于队列遵循先进先出的原则，最先添加的元素也是最先被移除的。

// 移除队列头部元素
dequeue() {
  // 队列为空，返回 undefined
    if (this.isEmpty()) {
      return undefined;
  }
  // 缓存队列头部的元素，以便该元素被移除后将它返回
  const result = this.items[this.lowestCount];
  delete this.items[this.lowestCount];
  // lowestCount 属性加 1，即当前头部元素被移除后，下一个头部元素在对象中的 key
  this.lowestCount++;
  return result;
}

head 查看队列头部元素

head 方法返回队列头部的元素，注意，这里只是查看，不是删除

head() {
  // 队列为空，返回 undefined
    if (this.isEmpty()) {
      return undefined;
  }
  // lowestCount 作为键名来获取元素
  return this.items[this.lowestCount];
}

tail 查看队列尾部元素

tail() {
  if (this.isEmpty()) {
      return undefined;
  }
    return this.items[this.count - 1];
}

isEmpty 判断队列是否为空

isEmpty 方法用来判断队列是否为空，如果队列为空，返回true，否则返回 false

isEmpty() {
    return this.count - this.lowestCount === 0
  // return this.size() === 0
}

clear 清空队列

clear 方法清空队列中的所有元素。我们可以调用 deqeue 方法直到它返回 undefined，也可以简单地将队列中的属性值重设为和构造函数中的一样。

clear() {
    this.items = {};
  this.count = 0;
  this.lowestCount = 0;
}

size 返回队列的大小

size 方法返回队列的大小，即返回队列中有多少个元素

size() {
  // count 只会增加，不会减少，lowestCount 是元素在对象中的key
  // count 与 lowestCount 两者的差值就是队列中元素的个数
    return this.count - this.lowestCount;
}

print 打印队列

print 方法负责以字符串的形式将队列打印出来

print() {
    if (this.isEmpty()) {
      return '';
  }
  let objString = `${this.items[this.lowestCount]}`;
  for (let i = this.lowestCount + 1; i < this.count; i++) {
      objString = `${objString}, ${this.items[i]}`;
  }
  return objString;
}

完整代码

class Queue {
    constructor() {
      this.count = 0;
    this.lowestCount = 0;
    this.items = {};
  }
  enqueue(element) {
      this.items[this.count] = element;
    this.count++;
  }
  dequeue() {
      if (this.isEmpty()) {
        return undefined;
    }
    const result = this.items[this.lowestCount];
    delete this.items[this.lowestCount];
    this.lowestCount++;
    return result;
  }
  head() {
    if (this.isEmpty()) {
        return undefined;
    }
    // lowestCount 作为 键名来获取元素
      return this.items[this.lowestCount];
  }
  tail() {
    if (this.isEmpty()) {
        return undefined;
    }
      return this.items[this.count - 1];
  }
  isEmpty() {
      return this.count - this.lowestCount === 0;
  }
  clear() {
      this.items = {};
    this.count = 0;
    this.lowestCount = 0;
  }
  // count 只会增加，不会减少，lowestCount 是元素在对象中的 key
  // count 与 lowestCount 的差值就是队列中元素的个数
  size() {
      return this.count - this.lowestCount;
  }
  print() {
      if (this.isEmpty()) {
        return '';
    }
    let objString = `${this.items[this.lowestCount]}`;
    for (let i = this.lowestCount + 1; i < this.count; i++) {
        objString = `${objString}, ${this.items[i]}`;
    }
    return objString;
  }
}

基于数组的队列

我们使用ES6的类来创建一个基于数组的队列：

class Queue {
    constructor() {
      this.items = [];
  }
}

同样，我们为队列声明以下队列可用的方法：

enqueue(element) 向队列尾部添加一个新的元素
dequeue() 移除队列头部的元素
head() 查看队列头部的元素（注意：不是删除，只是查看）
tail() 查看队列尾部的元素（注意：不是删除，只是查看）
isEmpty() 判断队列是否为空
clear() 清空队列
size() 返回队列的大小
print() 打印队列

enqueue 向队列尾部添加元素

队列是基于数组来实现的，因此可以使用数组的 push 方法向队列尾部添加新元素

enqueue(element) {
  // 使用 数组的 push 方法向队列尾部添加新元素
    this.items.push(element);
}

dequeue 移除队列头部元素

队列基于数组实现，我们同样可以使用数组的 shift 方法来移除队列头部的元素

dequeue() {
 if (this.isEmpty()) {
     return undefined;
 }
 // 使用 数组 的 shift 方法移除队列头部元素
 return this.items.shift();
}

head 查看队列头部元素

head 方法返回队列头部元素，即数组的第一个元素。注意：这里只是查看元素，不是删除

head() {
  if (this.isEmpty()) {
      return undefined;
  }
    return this.items[0];
}

tail() 查看队列尾部元素

tail() {
    if (this.isEmpty()) {
      return undefined;
  }
  return this.items[this.items.length - 1]
}

isEmpty 判断队列是否为空

isEmpty 方法判断队列是否为空，要判断队列是否为空，只需要判断数组的长度是否为 0 即可

isEmpty() {
    return this.items.length === 0
}

clear 清空队列

clear 方法用于清空队列，即将数组重置为一个空数组

clear() {
    this.items = [];
}

size 返回队列的大小

size 方法返回队列的大小，即返回的是数组的长度

size() {
    return this.items.length;
}

print 打印队列

print 方法以字符串的形式将队列中的元素打印出来

pring() {
    return this.items.toString();
}

完整代码

class Queue {
    constructor() {
      this.items = []
  }
  enqueue(element) {
      this.items.push(element);
  }
  dequeue() {
      if (this.isEmpty()) {
        return undefined;
    }
    return this.items.shift();
  }
  head() {
      if (this.isEmpty()) {
        return undefined;
    }
    return this.items[0];
  }
  tail() {
      if (this.isEmpty()) {
        return undefined;
    }
    return this.items[this.items.length - 1]
  }
  isEmpty() {
      return this.items.length === 0;
  }
  clear() {
      this.items = [];
  }
  size() {
      return this.items.length;
  }
  print() {
      return this.items.toString();
  }
}

基于链表实现队列

队列的方法与基于Object对象和基于数组实现的队列一致，我们不再赘述。

class Queue {
    const linkList = new LinkList();
  // 入队列
    enqueue(element) {
    // 链表的 append 方法是向链表尾部添加元素
    // 对应于队列，就是在队列尾部添加元素
      return linkList.append(element);
  }
    // 出队列
    dequeue() {
    // 链表的 removeHead 方法是移除链表头部节点
    // 对应于队列，就是在队列头部移除元素
      return linkList.removeHead();
  }
    // 返回队首
  head() {
    // 链表的 head 方法返回的是链表的头节点
    // 对应于队列，就是返回队列的头部元素
      return linkList.head();
  }
    // 返回队尾
    tail() {
    // 链表的 tail 方法返回的是链表尾部的节点
    // 对应于队列，就是返回队列尾部的元素
      return linkList.tail();
  }
    // 判断队列是否为空
    isEmpty() {
    // 链表的 isEmpty 方法判断链表是否为空
    // 对应于队列，就是判读队列是否为空
      return link.isEmpty();
  }
    // 清空队列
    clear() {
    // 链表的 clear 方法清空链表
    // 对应于队列，就是清空队列
      linkList.clear();
  }
    // 队列长度
    size() {
    // 链表的 size 方法返回的是链表的长度
    // 对应于队列，就是返回队列的长度
      return linkList.size()
  }
    // 打印队列
    print() {
    // 链表的 toString 方法返回链表的字符串形式
    // 对应于队列，就是返回队列的字符串形式
      return linkList.toString()
  }
}

队列的应用

约瑟夫环

有一个长度为 a 的数组，存放 0~99 的数字，要求每隔两个数删掉一个数，到末尾时循环至开头继续进行删除操作，求最后一个被删掉的数

思路分析

前10个数是 0 1 2 3 4 5 6 7 8 9，所谓每隔两个数删掉一个数，其实就是把 2、5、8 删除，也就是每 3 个数中删除最后一个数。

我们使用队列来解决这个问题，先把这 100 个数放入队列中，然后使用 while 循环，当队列里只剩一个元素时，就终止 while 循环。我们定义一个 index 变量从 0 开始计数，算法步骤如下：

从队列头部删除一个元素，然后 index 变量加 1
判断 index % 3 的结果是否为 0，如果为 0，就说明这个元素是需要删除的元素，如果不等于0，就不是需要被删除的元素，则把它添加到队列的尾部

不停的有元素被删除，最终队列里只有一个元素，此时 while 循环终止，队列里剩下的元素就是最后一个被删除的元素

算法实现

const delRing = (arrList) => {
  const queue = new Queue();
  // 将数组里的元素放入队列中
  for (let i = 0; i < arrList.length; i++) {
    queue.enqueue(arrList[i]);
  }
  // index 变量用来计数
  let index = 0;
  while (queue.size() !== 1) {
    // 从队列中弹出一个元素，判断是否需要删除
    const item = queue.dequeue();
    index += 1;
    // 每隔两个就要删除一个，那么不是被删除的元素就放回到队列尾部
    if (index % 3 != 0) {
      queue.enqueue(item);
    }
  }
  return queue.head()
}

测试结果：

const arrList = []
for (let i = 0; i < 100; i++) {
  arrList.push(i)
}
// 最后一个被删除的元素是 90
delRing(arrList) // 90

斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……

斐波那契数列通常用 F(n) 表示，该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1

斐波那契数列是一个非常经典的问题，有着各种各样的解法，比较常见的是递归算法，其实也可以使用队列来实现。

思路分析：
先将 0 和 1 添加到队列中，然后使用 while 循环，使用 index 变量来计数，当 index < n - 2 时终止循环：

使用 dequeue 方法从队列头部删除一个元素，，该元素为 del_item
使用 head 方法获得队列头部的元素，该元素为 head_item
del_item + head_item = next_item，将 next_item 放入队列，注意：只能从队列尾部添加元素
然后将变量 index 加 1

当循环结束时，队列里面会有两个元素，先使用 dequeue 方法删除头部元素，剩下的那个元素就是我们要计算的第 n 项的结果

算法实现：

const fibonacci = (n) => {
    queue = new Queue();
  // index 变量用来计数
  let index = 0;
  // 先将 斐波那契数列 的前两个数 0 和 1 放入队列中
  queue.enqueue(0);
  queue.enqueue(1);
  while(index < n - 2) {
    // 从队列中删除头部元素
      const del_item = queue.dequeue();
    // 获取队列中的头部元素
    const head_item = queue.head();
    // 计算两个元素相加的结果
    const next_item = del_item + head_item;
    // 将计算结果放入队列中
    queue.enqueue(next_item);
    index += 1;
  }
  queue.dequeue();
  return queue.head()
}
console.log(fibonacci(8))  // 13

用队列实现栈

在数据结构与算法学习之栈一文中，我们提到栈可以使用 JavaScript 中的数组和 Object对象来实现，其实栈也可以使用队列来实现。

队列的特点是先进先出，而栈的特点是先进后出，两者对数据的管理模式刚好是相反的，但是却可以使用两个队列来实现一个栈。

思路分析：
我们将两个队列分别命名为 queue_1、queue_2：

push 实现 push 方法时，如果两个队列都为空，那么默认向 queue_1 里添加元素；如果有一个队列不为空，则向这个不为空的队列里添加元素；
top 实现 top 方法时，两个队列，或者都为空，或者有一个不为空，只需要返回不为空的队列的尾部元素即可；
pop pop 方法的实现是比较复杂的，pop 方法要删除的是栈顶元素，但这个栈顶元素其实是队列的尾部元素。每一次 pop 操作时，将不为空的队列里的元素依次删除并放入到另一个队列中，直到这个不为空的队列里只剩下一个元素，删除这个元素，其余的元素就都放到之前为空的队列中了。

在具体的实现中，我们额外定义两个变量 data_queue 和 empty_queue，data_queue 始终指向那个不为空的队列，empty_queue 始终指向那个为空的队列。

算法实现：

class QueueStack {
  constructor() {
    this.queue_1 = new Queue();
    this.queue_2 = new Queue();
    this.data_queue = null; // 放数据的队列
    this.empty_queue = null; // 空队列，备份使用
  }
  init_queue = () => {
    if (this.queue_1.isEmpty() && this.queue_2.isEmpty()) {
      this.data_queue = this.queue_1;
      this.empty_queue = this.queue_2;
    } else if (this.queue_1.isEmpty()) {
      this.data_queue = this.queue_2;
      this.empty_queue = this.queue_1;
    } else {
      this.data_queue = this.queue_1;
      this.empty_queue = this.queue_2;
    }
  }
  push(item) {
    this.init_queue();
    this.data_queue.enqueue(item);
  }
  // top 方法返回栈顶元素，实质返回的是队列的尾部元素
  top() {
    this.init_queue();
    return this.data_queue.tail()
  }
  pop() {
    this.init_queue();
    // 将 不为空队列 data_queue 中的元素依次出队列并放入为空的 empty_queue 队列中
    while (this.data_queue.size() > 1) {
      const del_item = this.data_queue.dequeue()
      this.empty_queue.enqueue(del_item)
    }
    // 当 data_queue.size() 为 1 时，data_queue 中只剩一个元素，也就是队列的尾部元素
    // 将队列的尾部元素返回，即为栈顶元素
    return this.data_queue.dequeue()
  }
}
var q_stack = new QueueStack();
q_stack.push(1);
q_stack.push(2);
q_stack.push(4);
console.log(q_stack.top());            //    栈顶是    4
console.log(q_stack.pop());            //    移除    4
console.log(q_stack.top());            //    栈顶变成    2
console.log(q_stack.pop());            //    移除    2
console.log(q_stack.pop());            //    移除    2

打印杨辉三角

杨辉三角形，又称帕斯卡三角形、贾宪三角形、海亚姆三角形、巴斯卡三角形，是二项式系数的一种写法，形似三角形，在中国首现于南宋杨辉的《详解九章算法》得名，书中杨辉说明是引自贾宪的《释锁算书》，故又名贾宪三角形。前 9 行写出来如下：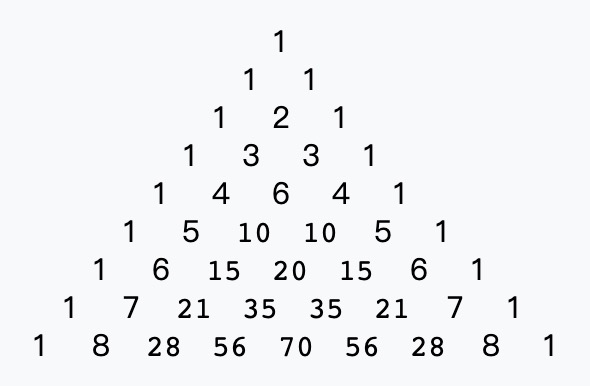

使用队列打印出杨辉三角的前 n 行，其中 n >= 1，思路分析如下：

杨辉三角中的每一行，都依赖于上一行，假设在队列里存储第 n - 1 行的数据，输出第 n 行时，只需要将队列里的数据依次出队列，进行计算得到下一行的数值并将计算所得放入到队列中。

计算公式：f[i][j] = f[i - 1][j - 1] + f[i-1][j] ，i 代表行数，j 代表一行的第几个数，如果 j 等于 0 或者 j = i，则 f[i][j] = 1

但是将计算所得放入队列中时，队列中保存的是两行的数据，一部分是第 n - 1 行的数据，另一部分是刚刚计算出来的第 n 行数据，需要有办法将这两行数据分隔开。

分开的方式有两种：
一种是使用 for 循环进行控制，在输出第 5 行时，其实只有 5 个数据可以输出，那么就可以使用 for 循环控制调用 enqueue 的次数，循环 5 次后，队列里存储的就是计算好的第 6 行的数据

第二种方法是每一行的数据后面多存储一个 0 ，使用这个 0 作为分界点，如果 dequeue 返回的是 0 ，就说明这一行已经全部输出，此时，将这个 0 追加到队列的尾部。

算法实现

实现方法一**
使用两层for 循环，第一层 for 循环控制打印的层数，第二层 for 循环控制打印每层的元素

function print_yanghui_triangle(n) {
  const queue = new Queue();
  queue.enqueue(1);
  // 第一层 for 循环控制打印几层
  for (let i = 1; i <= n; i++) {
    const space = Math.floor((n - i))
    let line = new Array(space).fill(" ").toString().replace(/,/g, " ");
    let pre = 0;
    // 第二层 for 循环控制打印第 i 层的元素
    for (let j = 0; j < i; j++) {
      const item = queue.dequeue();
      line += item + "  ";
      // 计算下一行的 值
      const value = item + pre;
      pre = item;
      queue.enqueue(value);
      // 每一次的最后一个数字是 1
      if (j === i - 1) {
        queue.enqueue(1);
      }
    }
    // 每一层的最后一个数字是 1，上面的 for 循环没有计算最后一个数
    // queue.enqueue(1);
    console.log(line)
  }
}

实现方法二
每一行的数据后面多存储一个 0 ，使用这个 0 作为分界点

function print_yanghui_triangle2(n) {
  const queue = new Queue();
  queue.enqueue(1);
  // 0 作为每一行数据的分节点
  queue.enqueue(0);
  for (let i = 1; i <= n; i++) {
    const space = Math.floor((n - i))
    let line = new Array(space).fill(" ").toString().replace(/,/g, " ");
    let pre = 0;
    while (true) {
      const item = queue.dequeue();
            // 使用 0 将每一行的数据分隔开，遇到 0 不输出
      if (item === 0) {
        queue.enqueue(1);
        queue.enqueue(0);
        break
      } else {
        // 计算下一行的值
        line += item + "  ";
        const value = item + pre;
        pre = item;
        queue.enqueue(value)
      }
    }
    console.log(line)
  }
}

参考资料
书籍：《JavaScript数据结构与算法》