题目

题目来源：力扣（LeetCode）

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  • 例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。


示例 1：

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3 。

示例 2：

输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc” ，它的长度为 3 。

示例 3：

输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0 。

思路分析

最长公共子序列问题是典型的二维动态规划问题。下面讲解动态规划的做法。

1、状态定义

dp[i][j]：表示字符串 text1 的 [0, i - 1] 区间 和 字符串2 的 [0, j - 1] 区间的最长公共子序列的长度

为什么要定义长度为[0, i - 1]的字符串text1，这样定义是为了后面代码实现方便；定义为为长度为[0, i]的字符串text1也可以

2、状态转移方程

根据 text1[i - 1] 与 text2[j - 1] 是否相同，分为两种情况：

  • text1[i - 1] 与 text2[j - 1]相同

也就是说两个字符串的最后一位相等，那么问题就转化成了字符串text1的[0, i - 1]区间和字符串text2的[0,j - 1]区间的最长公共子序列长度再加上一，因此 dp[i][j] = dp[i - 1][j - 1] + 1

  • text1[i - 1] 与 text2[j - 1]不相同

也就是说两个字符串的最后一位不相等，那么字符串 text1 的 [0, i - 1] 区间和字符串 text2 的 [0, j -1] 区间的最长公共子序列长度无法延长，考虑以下两种情况：

  • text1[0, i - 2] 与 text2[0, j - 1] 的最长公共子序列
  • text1[0, i - 1] 与 text2[0, j - 2] 的最长公共子序列

取两者中的最大值，即dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

由以上两种情况，可得状态转移方程：
dp[i][j] = dp[i - 1][j - 1] + 1 ,当text1[i] == text2[j]
dp[i][j] = max(dp[i - 1][j],dp[i][j - 1])，当text1[i] != text2[j]

3、状态初始化

test1[0, i - 1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0
同理：test2[0, j - 1]和空串的最长公共子序列自然是0，所以dp[0][j] = 0

其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

4、确定遍历顺序
从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：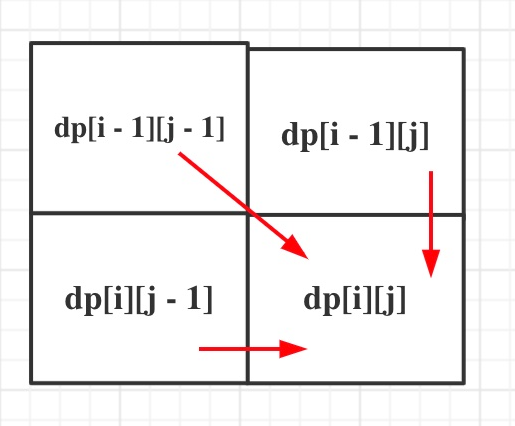
image.png

那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

代码实现

  1. /**
  2.  * @param {string} text1
  3.  * @param {string} text2
  4.  * @return {number}
  5.  */
  6. var longestCommonSubsequence = function (text1, text2) {
  7.   const m = text1.length, n = text2.length;
  8.   // 初始化二维数组
  9.   const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
  10.   // dp[i][j]表示text1前i位和text2前j位的最长公共子序列的长度
  11.   for (let i = 1; i <= m; i++) {
  12.     const c1 = text1[i - 1];
  13.     for (let j = 1; j <= n; j++) {
  14.       const c2 = text2[j - 1];
  15.       if (c1 === c2) {
  16.         // 如果相等说明最长字串长度就得＋1
  17.         dp[i][j] = dp[i - 1][j - 1] + 1
  18.       } else {
  19.         //若不相等就取最大值
  20.         dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
  21.       }
  22.     }
  23.   }
  24.   return dp[m][n];
  25. };

参考阅读： https://leetcode-cn.com/problems/longest-common-subsequence/solution/zui-chang-gong-gong-zi-xu-lie-tu-jie-dpz-6mvz/ https://leetcode-cn.com/problems/longest-common-subsequence/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-dpzi-zqa9q/