题目

题目来源：力扣（LeetCode

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：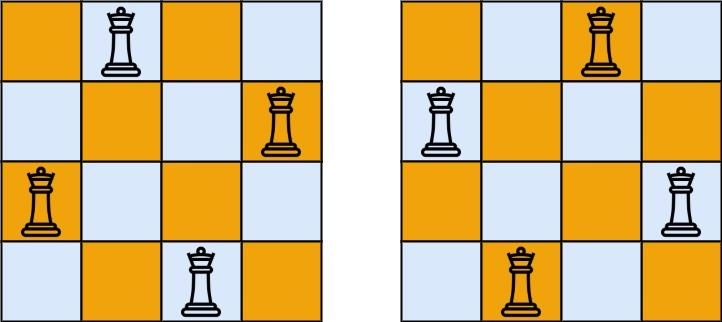
image.png

输入：n = 4
输出：[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[[“Q”]]

思路分析

皇后彼此不相互攻击，就是让皇后横直斜走，两个皇后不能在同一行，同一列，以及同一条斜线上。

  1. 每一行，选出一个格子，置为Q，一行行地往下选择，第一行有四种选择
  2. 在选择下一行的皇后的时候，为了避免列的冲突，有三种选择：
  3. 继续选下去，可能会遇到对角线的冲突，继续选下去没有意义，得出不合法的解，需要回溯。
  1. /**
  2.  * @param {number} n
  3.  * @return {string[][]}
  4.  */
  5. const solveNQueens = (n) => {
  6.   const board = new Array(n);
  7.   for (let i = 0; i < n; i++) { // 棋盘的初始化
  8.     board[i] = new Array(n).fill('.');
  9.   }
  10.   const cols = new Set(); // 列集，记录出现过皇后的列
  11.   const diag1 = new Set(); // 正对角线集
  12.   const diag2 = new Set(); // 反对角线集
  13.   const res = [];
  15.   // row 控制棋盘的行
  16.   const helper = (row) => {
  17.     if (row == n) {
  18.       const stringsBoard = board.slice();
  19.       for (let i = 0; i < n; i++) {
  20.         stringsBoard[i] = stringsBoard[i].join('');
  21.       }
  22.       res.push(stringsBoard);
  23.       return;
  24.     }
  26.     // 递归深度就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列，确定了放置皇后的位置。
  27.     // 每次都是要从新的一行的起始位置开始搜，所以都是从0开始。
  28.     for (let col = 0; col < n; col++) {
  29.       // 如果当前点的所在的列，所在的对角线都没有皇后，即可选择，否则，跳过
  30.       if (!cols.has(col) && !diag1.has(row + col) && !diag2.has(row - col)) {
  31.         /** 做选择 */
  32.         board[row][col] = 'Q'; // 放置皇后
  33.         cols.add(col); // 记录放了皇后的列
  34.         diag1.add(row + col); // 记录放了皇后的正对角线
  35.         diag2.add(row - col); // 记录放了皇后的负对角线
  36.         /** 进入下一行决策 */
  37.         helper(row + 1);
  38.         // 每次我们选择把这个位置放置皇后的时候，如果最终不能成功，那么返回的时候我们就还要把这个位置还原。这就是回溯算法，也是试探算法
  39.         /** 撤销选择 */
  40.         board[row][col] = '.'; // 撤销该点的皇后
  41.         cols.delete(col); // 对应的记录也删一下
  42.         diag1.delete(row + col);
  43.         diag2.delete(row - col);
  44.       }
  45.     }
  46.   };
  47.   helper(0);
  48.   return res;
  49. };
  51. // https://www.cnblogs.com/labuladong/p/12320463.html
  52. // https://leetcode-cn.com/problems/n-queens/solution/nhuang-hou-jing-dian-hui-su-suan-fa-tu-wen-xiang-j/