题目

题目来源：力扣（LeetCode）

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：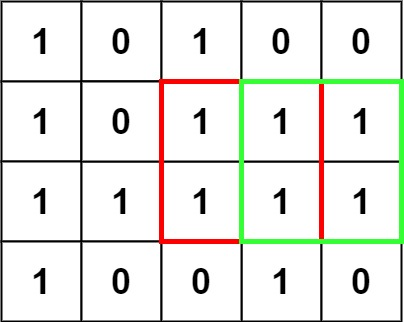
image.png
输入：matrix = [[“1”,”0”,”1”,”0”,”0”],[“1”,”0”,”1”,”1”,”1”],[“1”,”1”,”1”,”1”,”1”],[“1”,”0”,”0”,”1”,”0”]]
输出：4

示例 2：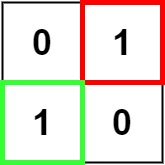
image.png
输入：matrix = [[“0”,”1”],[“1”,”0”]]
输出：1

示例 3：

输入：matrix = [[“0”]]
输出：0

思路分析

动态规划

1、状态定义
定义二维数组 dp[][]，其中 dp[i][j] 表示的是在矩阵中以左边 (i, j) 为右下角，且只包含 1的最大正方形边长。

2、确定递推公式
如果想要求 dp 中的每个元素值，那么对于矩阵中的每个位置 (i, j)，检查矩阵中该位置的值 matrix[i][j]

如果matrix[i][j]的值是0，根据题意，该值就没法构成正方形，所以dp[i][j]=0。

如果matrix[i][j]的值是1，说明它可以构成一个正方形，并且这个正方形的边长最小是1。

  • 如果我们想求最大值，还需要判断他左上角的值 dp[i - 1][j - 1]，如果dp[i - 1][j - 1]是 0，那么以坐标(i, j)为右下角的最大正方形边长就是1，如下图所示：

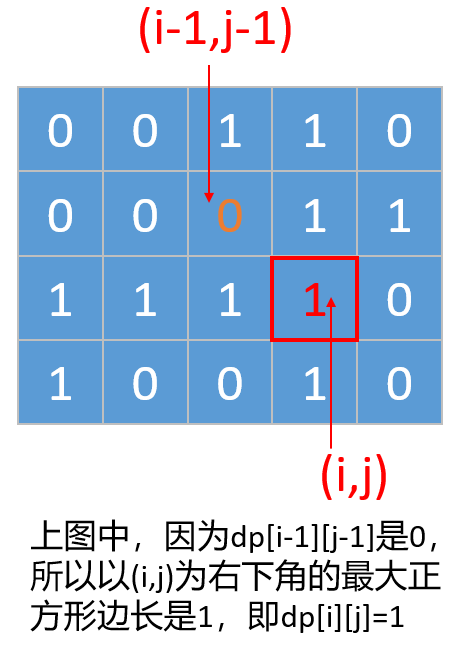
image.png

  • 如果左上角的值 dp[i - 1][j - 1]不是 0，也就是说它也可以构成正方形，那么以坐标 (i, j) 为右下角有可能可以构成一个更大的正方形。为啥说是有可能，因为如果我们要确定它能不能构成一个更大的正方形，还要往它的上边和左边找，如下图所示：

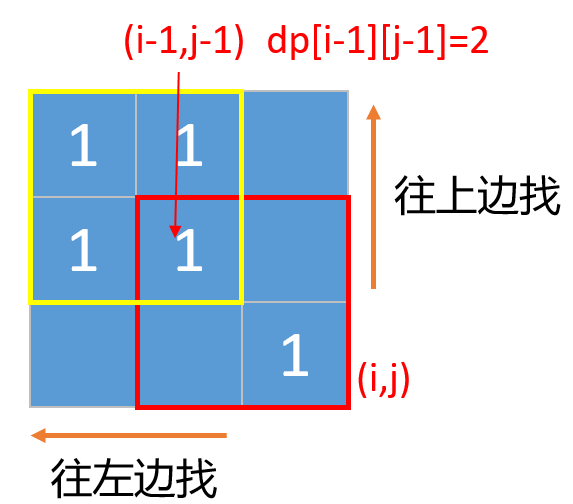
image.png

  • 有可能是下面这种情况，就是左边或者上边的某一个高度小于dp[i - 1][j - 1]的值，要想构成最大的正方形我们只能取最小的。

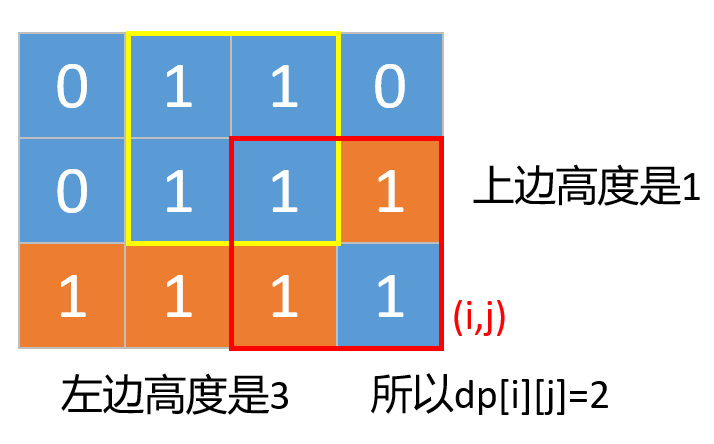
image.png

  • 也有可能是下面这种，就是左边和上边的高度都不小于 dp[i - 1][j - 1] 的值。

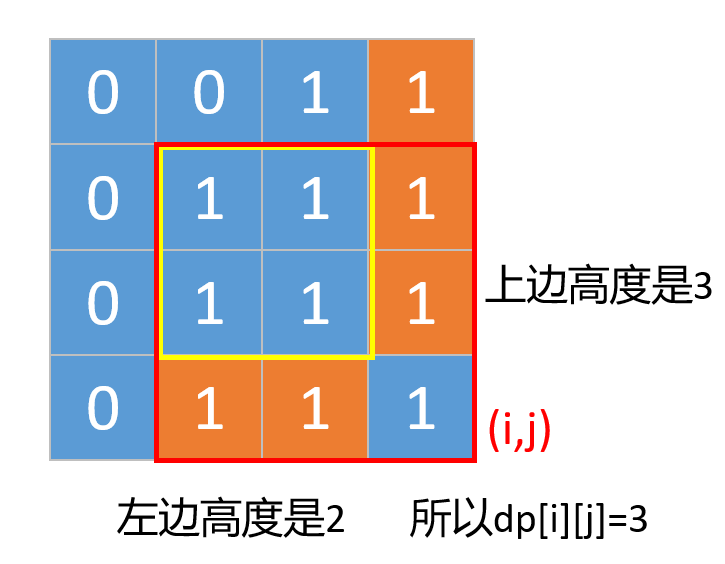
image.png
所以我们可以得出结论，如果(i,j)是1，那么以他为右下角的最大正方形边长是
[dp[i - 1][j - 1]，上边的高度，左边的高度]这3个中最小的 +1。

因此我们可以找出递推公式：

如果坐标(i, j)的值为 0，则**dp[i][j]=0;**
如果坐标(i, j)的值为1，则**dp[i][j]=min(dp[i - 1][j],dp[i][j - 1],dp[i - 1][j - 1]) + 1;**

3、状态初始化
考虑边界条件，如果 i 和 j 中至少有一个为 0，则以坐标 (i, j) 为右下角的最大正方形的边长只能是 1，因此 dp[i, j] = 1

代码实现

  1. /**
  2.  * @param {character[][]} matrix
  3.  * @return {number}
  4.  */
  5. var maximalSquare = function (matrix) {
  6.   let m = matrix.length
  7.   let n = matrix[0].length
  8.   const dp = new Array(m).fill(0).map(() => new Array(n).fill(0))
  9.   let max = 0 // 正方形的最大边长
  11.   // 矩阵只有一列
  12.   for (let i = 0; i < m; i++) {
  13.     if (matrix[i][0] === '1') {
  14.       dp[i][0] = 1
  15.       max = Math.max(max, dp[i][0])
  16.     }
  17.   }
  19.   // 矩阵只有一行
  20.   for (let j = 0; j < n; j++) {
  21.     if (matrix[0][j] === '1') {
  22.       dp[0][j] = 1
  23.       max = Math.max(max, dp[0][j])
  24.     }
  25.   }
  27.   // 遍历矩阵，寻找以坐标 (i, j) 为右下角的最大正方形边长
  28.   for (let i = 1; i < m; i++) {
  29.     for (let j = 1; j < n; j++) {
  30.       if ((matrix[i][j] === '1')) {
  31.         // 递推公式 min[dp[i - 1][j - 1], 上边的高度, 左边的高度] + 1
  32.         dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
  33.         max = Math.max(max, dp[i][j])
  34.       }
  35.     }
  36.   }
  37.   return max * max
  38. };

参考阅读 https://leetcode-cn.com/problems/maximal-square/solution/zui-da-zheng-fang-xing-by-leetcode-solution/ https://leetcode-cn.com/problems/maximal-square/solution/shu-ju-jie-gou-he-suan-fa-dong-tai-gui-h-q9my/