不同的二叉搜索树 II

题目

题目来源：力扣（LeetCode）

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：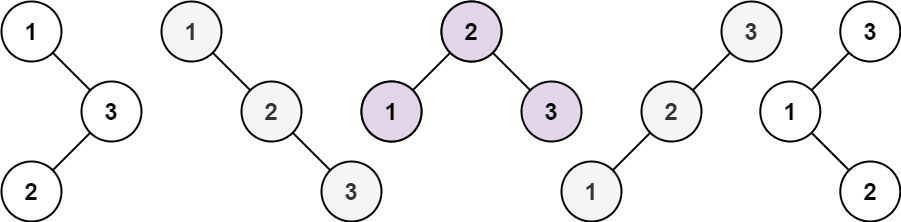

输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例 2：

输入：n = 1
输出：[[1]]

思路分析

二叉搜索树的关键性质是：根节点的值大于左子树所有节点的值，小于右子树所有节点的值，且左子树和右子树也同样为二叉搜索树。

假设当前序列长度为 n ，当我们枚举的根节点的值为 i ，根据二叉搜索树的性质我们可以知道：左子树的节点值的集合为 [1, i - 1] ，右子树的节点值的集合为 [i + 1, n] 。

例如当 n = 2，生成的二叉搜索树会有两中情况：
情况一，根节点为 1，根据二叉搜索树的性质，则左子树为 null，右子树为 2 ；
情况二，根节点为 2，根据二叉搜索树的性质，则左子树为 1 ，右子树为 null ；

我们可以使用递归来解决这道题。递归的入口即为 generateTrees(1, n)，出口为当 start > end 的时候，当前二叉搜索树为空，返回空节点即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number} n
 * @return {TreeNode[]}
 */
var generateTrees = function(n) {
  if (n === 0) return [];
  const getBSTnum = (left, right) => {
    // 根据二叉搜索树的性质，右子树的节点值一定比左子树的节点值大
    // 因此 left > right，则返回 [null]
    if (left > right) return [null];
    // 当左右子树值相等时，说明这个值就是父节点，这里 return [new TreeNode(left 或者 right)] 都是可以的
    if (left === right) return [new TreeNode(left)];
    const res = [];
    // 枚举可行的根节点
    for (let i = left; i <= right; i++) {
      // 根据二叉搜索树的性质，左子树的节点值都小于根节点，所以左子树的节点值集合为 [1, i - 1]
      // 获得所有可行的左子树集合
      const leftBst = getBSTnum(left, i - 1);
      // 根据二叉搜索树的性质，右子树的节点值都大于于根节点，所以左子树的节点值集合为 [i + 1, n]
      // 获得所有可行的右子树集合
      const rightBst = getBSTnum(i + 1, right);
      // 从左子树集合中选出一棵左子树，从右子树集合中选出一棵右子树，拼接到根节点上
      for (let leftKey of leftBst) {
        for (let rightKey of rightBst) { // 这里使用 for...of 循环，即使是 [null] 也可以遍历
          let root = new TreeNode(i);
          root.left = leftKey;
          root.right = rightKey;
          res.push(root)
        }
      }
    }
    return res;
  }
  return getBSTnum(1, n);
};