概念介绍

树是一种非线性的数据结构，是由 n(n>=0) 个节点组成的有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是它是根朝上，而叶朝下的。它具有以下的特点：

• 每个节点都只有有限个子节点或无子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；
• 树里面没有环路(cycle)

下面是一棵树的结构图：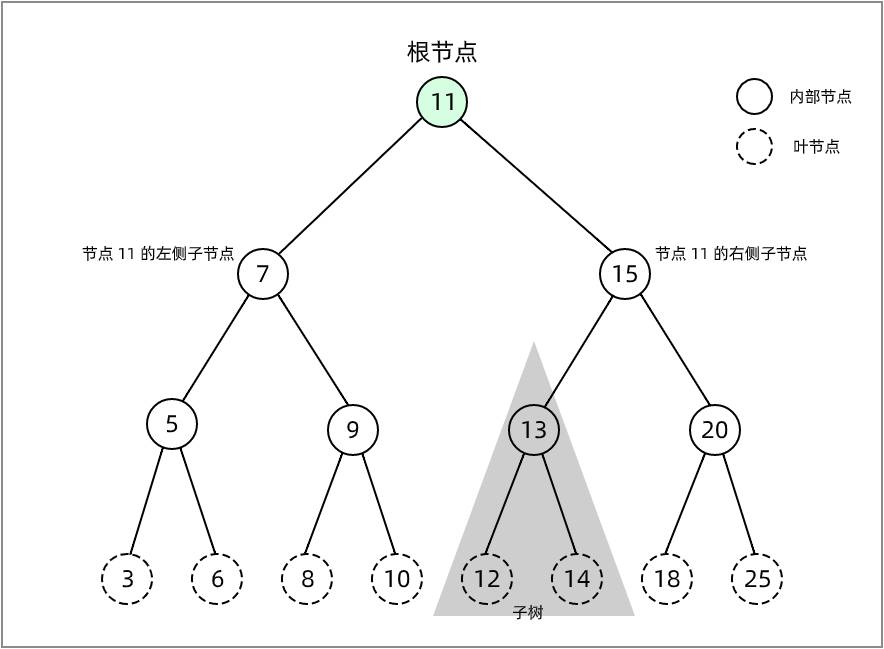

（图一）

节点

它包含数据项，和指向其它节点的指针，上图中的树，有 15 个节点

节点的度

一个节点所拥有的子树的个数称为该节点的度
在下图中，根节点 11 有两棵子树，因此根节点的度是 2；节点 13 也有两棵子树，因此它的度也是 2；而节点 3 没有子树，因此它的度为 0 。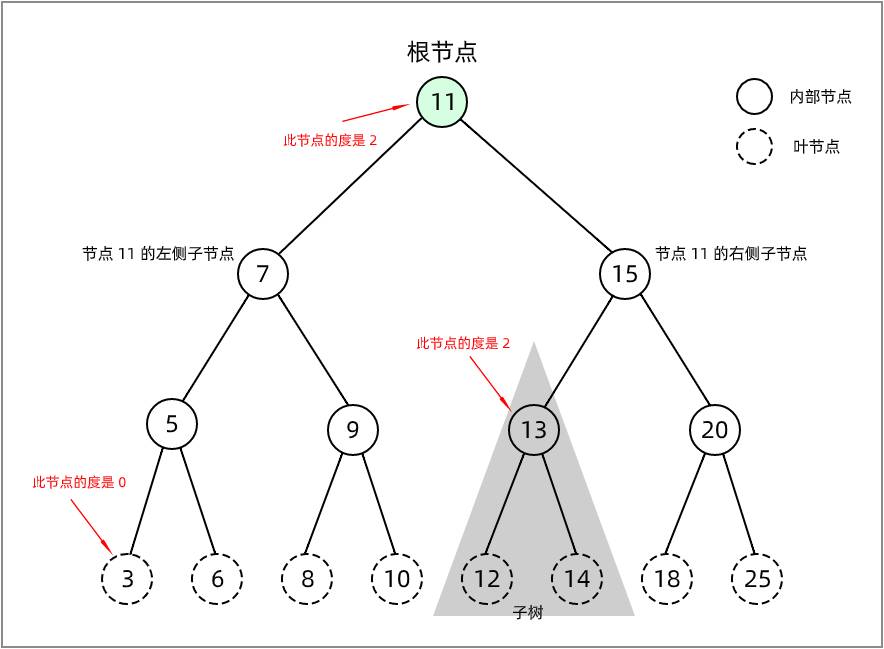

（图二）

叶节点

度为 0 的节点被称为 叶节点，如上图中的 3、6、8、10、12、14、18、25 节点都是叶节点

分支节点

除 叶节点 外的节点就是分支节点，如上图中的 11、7、15、5、9、13、20节点都是分支节点

子节点（孩子节点）

若节点x有子树，则这颗子树的根节点就是节点x的子节点，例如7、15 是 11 的根节点

父节点

若节点x有子节点，则 节点x 为子节点的父节点，如上图中的 11 是7、15的父节点，7是5、9的父节点，5是3、6的父节点

兄弟节点

同一个父节点的子节点互称为兄弟节点，如上图中的 7 和 15 是兄弟节点，5 和 9 是兄弟节点

祖先节点

从根节点到该节点所经过分支上的所有节点，如节点5，它的祖先节点为 11、7，又如节点3，它的祖先节点为 11、7、5

子孙节点

某一个节点的子女，以及这些子女的子女都是该节点的子孙节点，如节点7，它的子孙节点为5、3、6、9、8、10

节点所在的层次

从根开始定义起，根为第 1 层，根的子节点为第 2 层，以此类推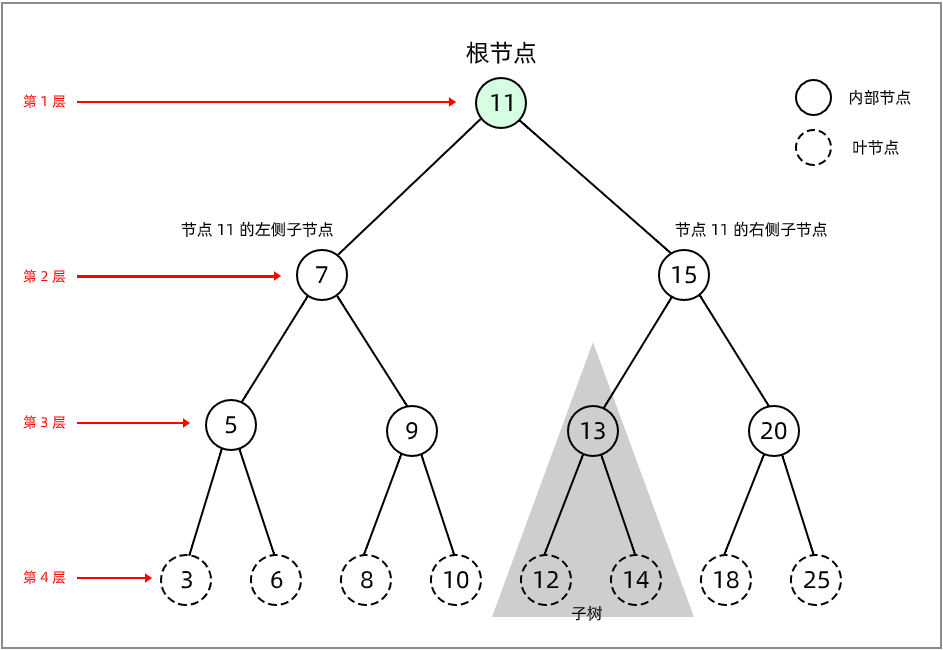

（图三）

树的深度

“深度”这个概念在生活中是从上往下度量的，比如水中鱼的深度，是从水平面开始度量的。所以，树这种数据结构的深度也是类似的，从根结点开始度量，计数起点为 1。

(深度、高度概念在不同的教材中有不同的定义，主要看高度深度的初值为几，有的为0，有的为1)

计算一个节点的深度，从根节点算起（记住从1开始计数，而不是0），到该节点所经过的节点数（包括此节点）为树的深度，如上图节点7 深度为2，节点3 的深度为4。

树中距离根节点最远的节点所处的层次就是树的深度，如上图中距离根节点最远的节点在第 4 层，因此树的深度是 4 。

树的高度

“高度”这个概念，其实就是从下往上度量，比如我们要度量第10层楼的高度、第13层楼的高度，起点都是地面。所以，树这种数据结构的高度也是一样，从叶子节点为1，向上开始计数，到此节点（包括此节点）的数值为此节点的高度，如图，节点7的高度为3，节点11的高度为4，节点11为根节点，根节点的高度即为树的高度。

树的度

树中节点的度的最大值称为树的度，如上图中，所有节点的度最大值为2，因此树的度就是2

森林

森林是 m (m >=0) 棵互不相交的树的集合。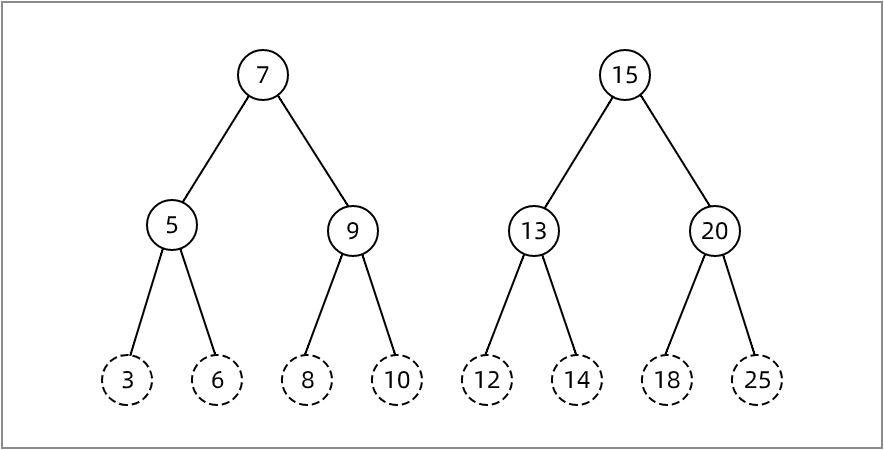
（图四）

上图中有两棵树，它们组成了一片森林。如果我们增加一个根节点11，让7、15成为这个根节点的子女，那么森林就变成了一棵树，如下图：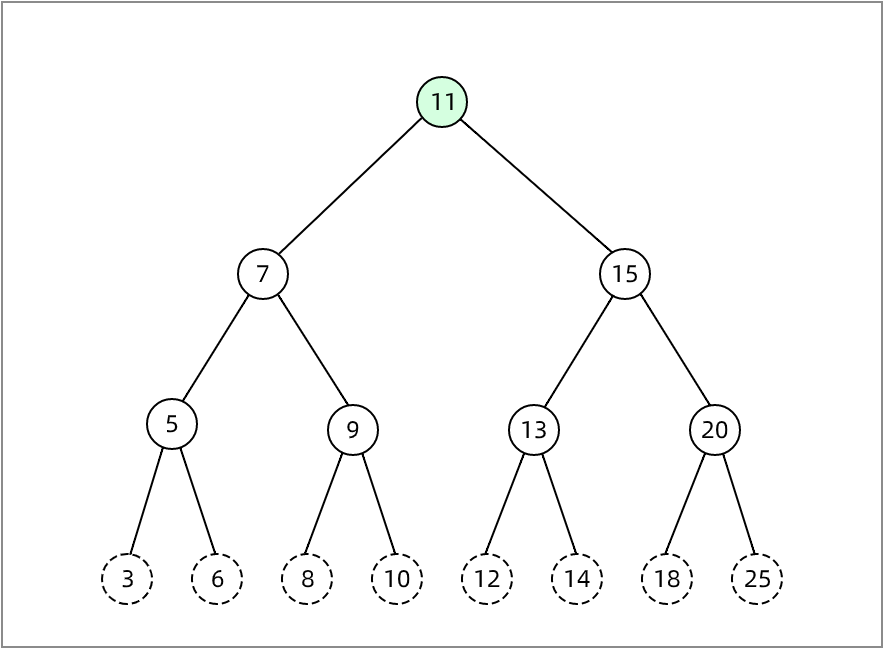

（图五）
如果我们删除了根节点，就变成了森林。

二叉树

二叉树是树的一种特殊情况。二叉树中的每个节点最多只能有两个子节点，一个是左侧子节点，另一个是右侧子节点。下图就是一棵二叉树。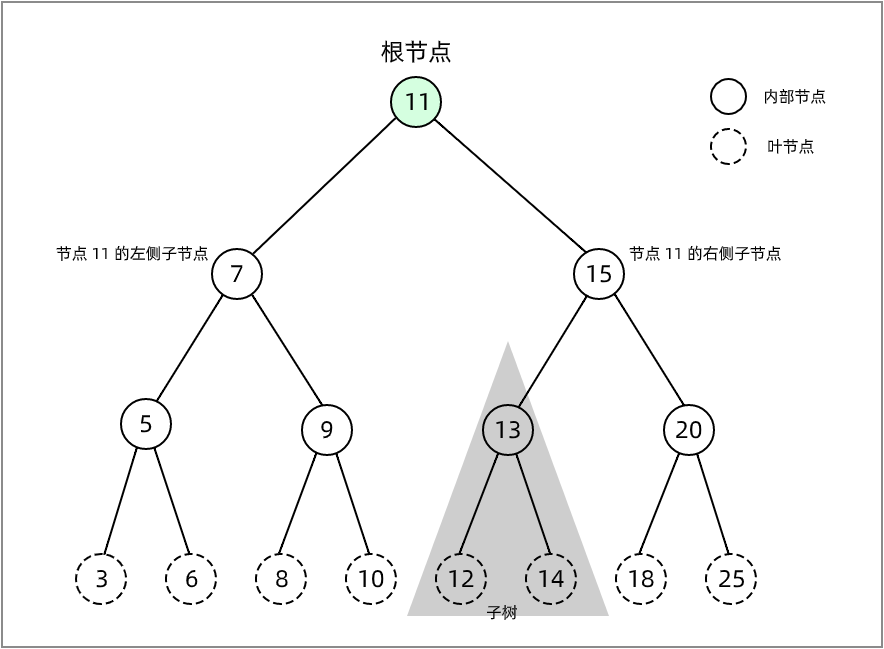

（图六）

如上图，节点7为根节点11的左侧子节点，节点15为根节点11的右侧子节点；节点5为节点7的左侧子节点，节点9为节点7的右侧子节点。

二叉树的特点

• 在二叉树的第 i (i >= 1) 层，最多有 2i-1 个节点
• 深度为 k(k>=0) 的二叉树，最少有 k 个节点，最多有 2k -1 个节点
• 对于一棵非空二叉树，叶节点的数量等于度为 2 的节点数量加1

满二叉树

深度为 k 的满二叉树，是有 2k-1 个节点的二叉树，每一层都达到了可以容纳的最大数量的节点。如图六就是一棵满二叉树。

完全二叉树

深度为 k 的完全二叉树，从第 1 层到第 k - 1 层都是满的，第 k 层，或是满的，或是从右向左连续缺若干个节点。如下图就是一棵完全二叉树。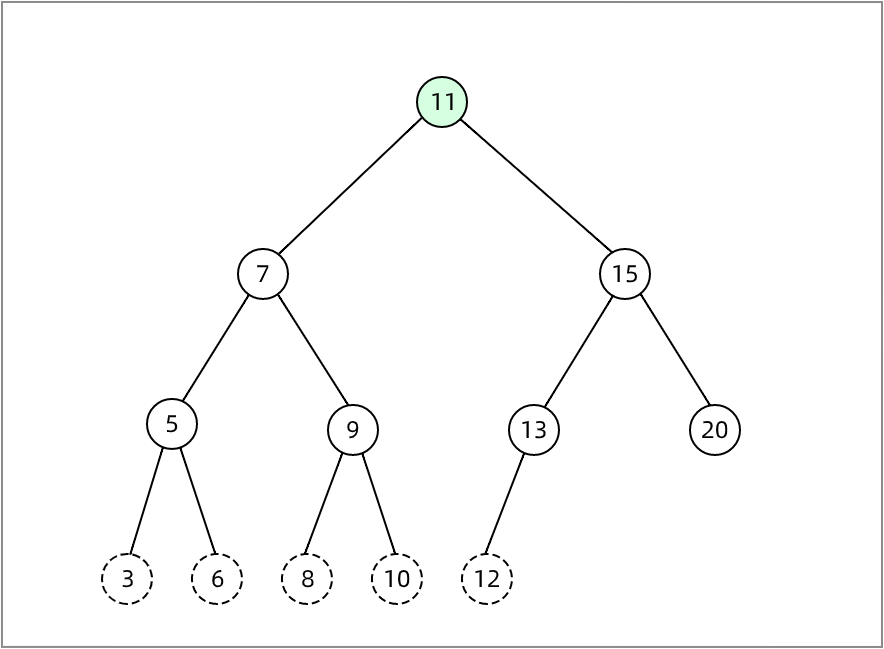

（图七）

二叉搜索树

二叉搜索树 (BST) ，又叫做二叉查找树、二叉排序树，是二叉树的一种，只允许在左侧节点存储比父节点小的值，在右侧节点存储比父节点大的值。如下图就是一棵二叉搜索树。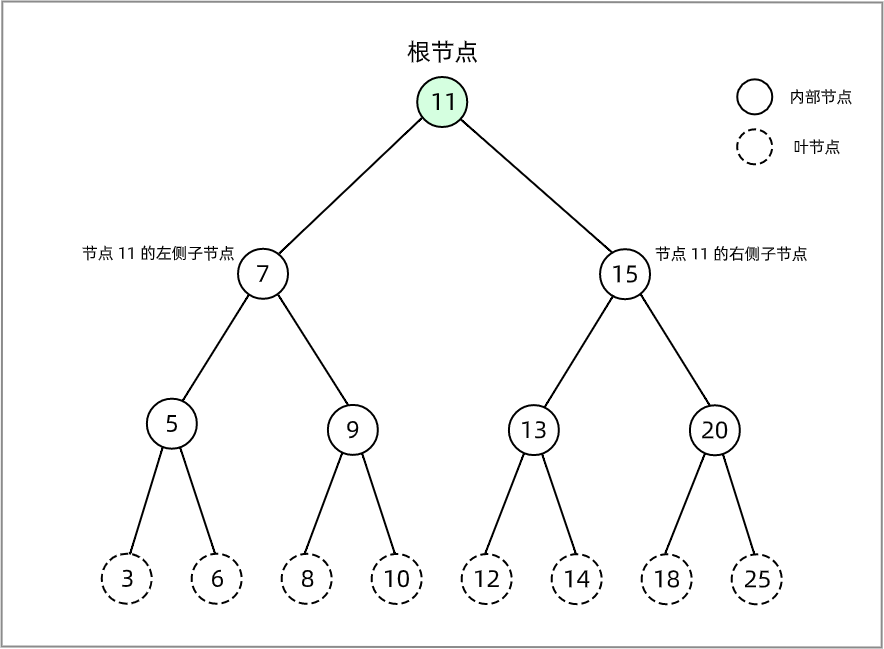

哈夫曼树

给定N个权值作为N个叶子节点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最小的二叉树。节点权值越大，距离根节点就越近。

AVL树

AVL 树首先是一棵二叉搜索树，但它具备自平衡的能力，它的左右子树都是 AVL 树，且左右子树的高度差的绝对值不超过1。添加或移除节点时，AVL 树会尽可能尝试转换为完全树。

红黑树

红黑树是一种自平衡二叉查找树。红黑树必须遵循下面的规则：

1. 每个节点不是红的就是黑的
2. 树的根节点是黑的
3. 所有的叶节点都是黑的（用NIL表示叶节点）
4. 每个红色节点的两个子节点都是黑色的（一个红节点不能有红的父节点或子节点）
5. 从任一节点到其每个叶子的所有路径都包含相同数量的黑色节点