题目

题目来源：力扣（LeetCode）

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：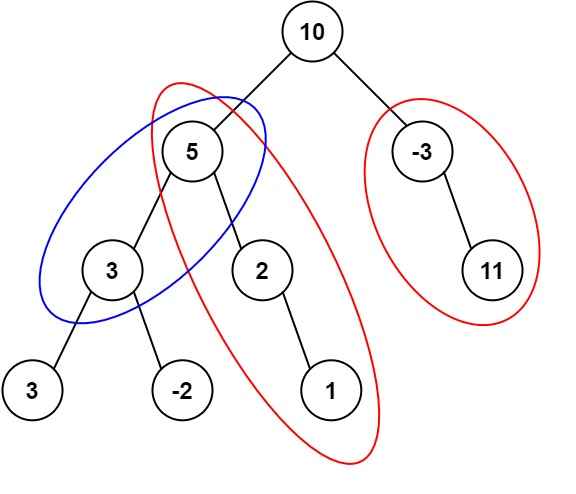
image.png

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

思路分析

前缀和 + 回溯

该道题主要用到了前缀和 与 回溯的思想。

在解题前，我们有四个点需要理解：

  • 前缀和的定义
  • 前缀和对本地有何作用
  • HashMap 存的是什么
  • 恢复状态代码的意义

前缀和的定义

从根节点向下，到某个节点的前缀和就是从根节点到某个节点的这条路径上所有节点的权值之和。(节点的权值：即节点上的数值)

在下图中：
节点 2 的前缀和为：1 + 2 = 3
节点 7 的前缀和为：1 + 2 + 4 + 7 = 14
节点 8 的前缀和为：1 + 2 + 4 + 8 = 15
节点 9 的前缀和为：1 + 2 + 5 + 9 = 17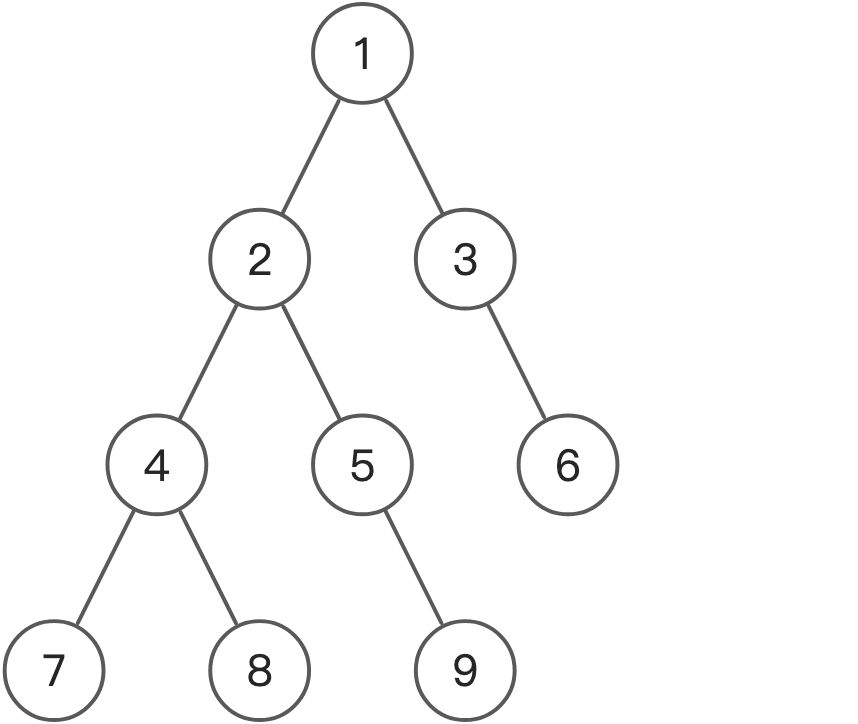
路径总和 III - 图2

前缀和对于本题有何作用

题目要求的是找出二叉树里节点值之和等于 targetSum 的 路径 的数目

两节点值之和 = 两节点的前缀和之差

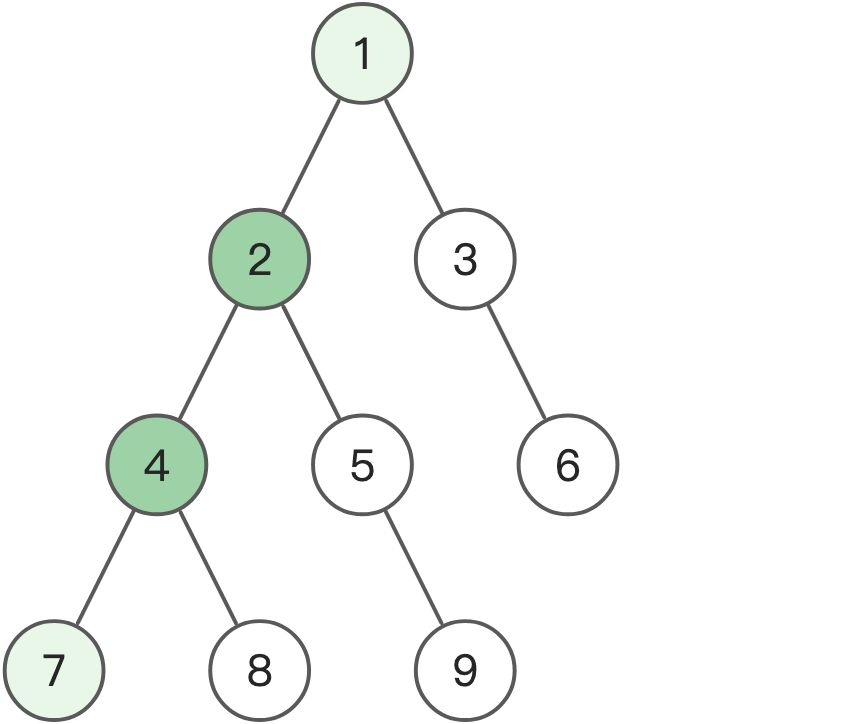
路径总和 III - 图3
假设 targetSum 的 6，即节点值之和为 6：

  1. 节点 1 的前缀和为：1
  2. 节点 4 的前缀和为：1 + 2 + 4 = 7
  3. 节点4 与 节点1 的前缀和之差为：prefix(4) - prefix(1) = 7 - 1 = 6
  4. 所以 节点1 到节点4 之间有一条符合要求的路径 (2 -> 4)，使得该路径上的所有节点值之和为 6，如上图中节点2 和节点4 之间的路径。

理解了这个之后，我们将问题简化为：

从根节点开始往下遍历整棵树，记录每个节点的前缀和，寻找以中间节点开始，到当前节点，路径和为 targetSum 值的路径，统计符合要求的路径数

HashMap 存的是什么

HashMap 的 key 是前缀和，value 是该前缀和的出现的次数，记录数量是因为有可能会出现路径和相同的路径。

在下图中，前缀和为 1 的节点有两个：节点1 和 节点0
路径和为 2 的路径数就会有两条： 0 —> 2，2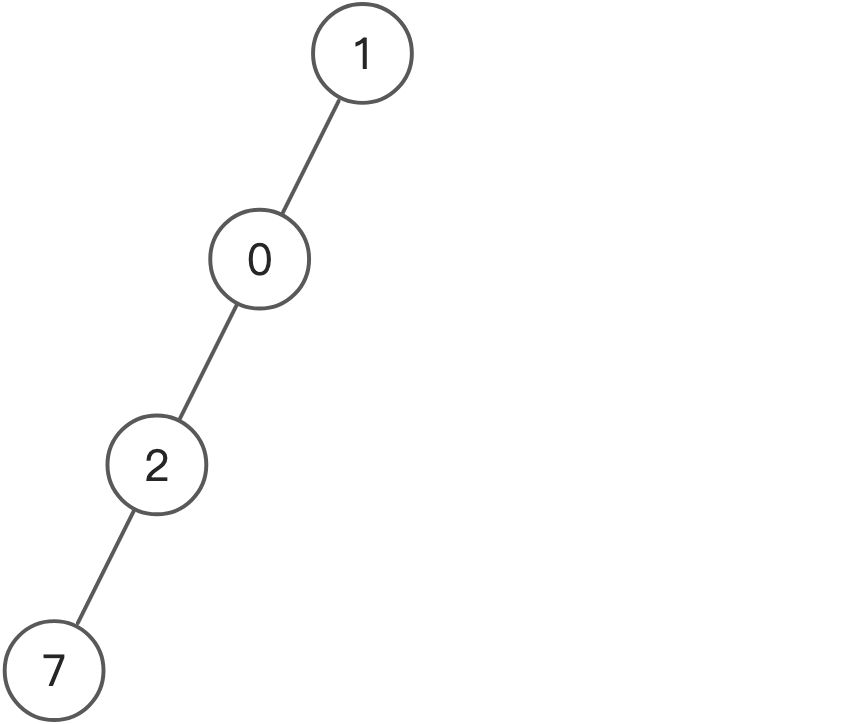
路径总和 III - 图4

恢复状态的意义

由于题目要求：路径方向必须是向下的（只能从父节点到子节点）
当我们讨论两个节点的前缀和差值时，有一个前提：

一个节点必须是另一个节点的祖先节点

换句话说，当我们把一个节点的前缀和信息更新到map里时，它应当只对其子节点们有效。
举个例子，下图中有两个值为2的节点（A, B)。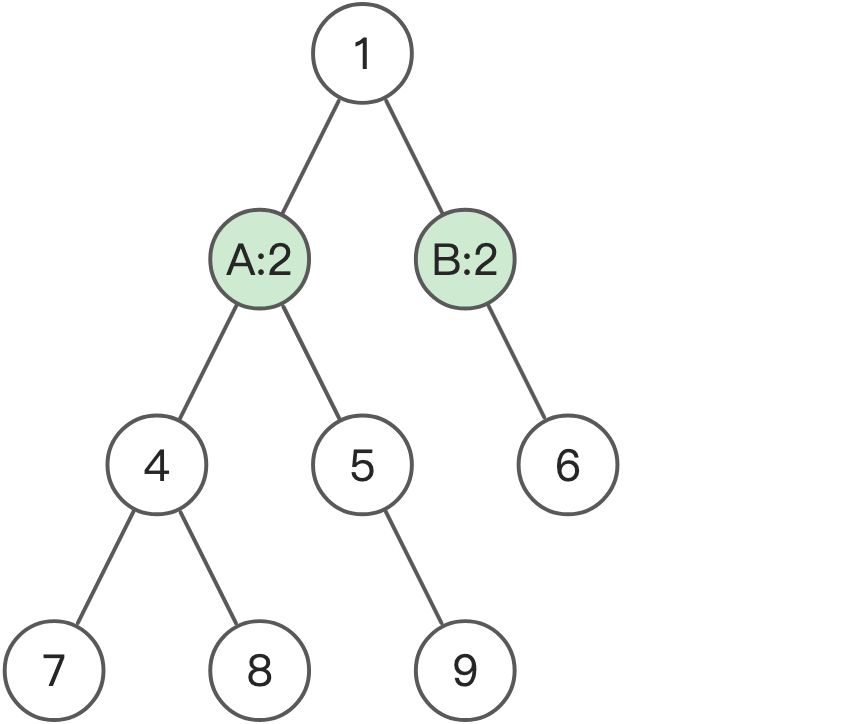
路径总和 III - 图5

当我们遍历到最右方的节点6时，对于它来说，此时的前缀和为2的节点只该有B, 因为从A向下到不了节点6(A并不是节点6的祖先节点)。

如果我们不做状态恢复，当遍历右子树时，左子树中A的信息仍会保留在map中，那此时节点6就会认为A, B都是可追溯到的节点，从而产生错误。

状态恢复代码的作用就是： 在遍历完一个节点的所有子节点后，将其从map中除去。

代码

  1. var pathSum = function (root, targetSum) {
  2.   // key 是前缀和，value是大小为 key 的前缀和出现的次数
  3.   const map = new Map();
  4.   // 前缀和为 0 时有一条路径
  5.   map.set(0, 1);
  6.   // 前缀和的递归回溯思路
  7.   return recursionPathSum(root, map, targetSum, 0)
  9.   /**
  10.    * 
  11.    * 前缀和的递归回溯思路
  12.    * 从当前节点反推到根节点(反推比较好理解，正向其实也只有一条)，有且仅有一条路径，因为这是一棵树
  13.    * 如果此前有和为pathSum-target,而当前的和又为 pathSum，两者的差就肯定为target了
  14.    * 所以前缀和对于当前路径来说是唯一的，当前记录的前缀和，在回溯结束，回到本层时去除，保证其不影响其他分支的结果
  15.    * @param node 树节点
  16.    * @param prefixSumMap 前缀和Map
  17.    * @param target 目标值
  18.    * @param pathSum 当前路径和(当前路径上的所有节点值之和)
  19.    * @returns 满足题解的解
  20.    */
  21.   function recursionPathSum(node, prefixSumMap, target, pathSum) {
  22.     // 递归终止条件
  23.     if (node == null) return 0;
  25.     let res = 0;
  26.     // 当前路径上所有节点值之和
  27.     pathSum += node.val;
  28.     // 看看root到当前节点这条路上是否存在节点前缀和加target为pathSum的路径
  29.     // 当前节点->root节点反推，有且仅有一条路径，如果此前有和为pathSum - target,而当前的和又为 pathSum,两者的差就肯定为target了
  30.     // pathSum - target相当于找路径的起点，起点的 sum + target = pathSum，当前点到起点的距离就是target
  31.     res += prefixSumMap.get(pathSum - target) || 0;
  32.     //此处是计数到当前节点为止有多少条自上而下的节点路径和等于pathSum，并将其存入map
  33.     // (亦或是更新pathSum对应的路径数，若先前有和值为pathSum的路径则取出其条数先前加上当前的一条)
  34.     prefixSumMap.set(pathSum, (prefixSumMap.get(pathSum) || 0) + 1);
  35.     // 遍历左子树
  36.     res += recursionPathSum(node.left, prefixSumMap, target, pathSum);
  37.     // 遍历右子树
  38.     res += recursionPathSum(node.right, prefixSumMap, target, pathSum);
  40.     // 回溯，回到本层，恢复状态，去除当前节点的前缀和数量
  41.     // 防止左边前缀树影响右边前缀树，左边前缀树可能有个为6，右边正好想要一个前缀树为6的，这样子就出错了
  42.     prefixSumMap.set(pathSum, prefixSumMap.get(pathSum) - 1);
  43.     // 结果是当前节点前缀树的个数加上左边满足的个数加右边满足的个数
  44.     return res;
  46.   }
  47. };

双递归

题目要求 路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的(只能从父节点到子节点) 。这就要求我们只需要去求三部分即可：

以当前节点作为头结点的路径数量
以当前节点的左孩子作为头结点的路径数量
以当前节点的右孩子作为头结点啊路径数量
将这三部分之和作为最后结果即可。

最后的问题是：我们应该如何去求以当前节点作为头结点的路径的数量？这里依旧是按照树的遍历方式模板，每到一个节点让sum-root.val，并判断sum是否为0，如果为零的话，则找到满足条件的一条路径。

  1. var pathSum = function (root, targetSum) {
  2.   const recursion = (root) => {
  3.     // 从根节点起，符合的有要求的递归
  4.     if (!root) return 0
  5.     // 内层递归
  6.     const dfs = (cRoot, sum) => {
  7.       // 从当前节点为起点，符合条件的格式
  8.       if (!cRoot) return 0
  9.       // 每到一个节点让 sum - root.val，并判断当前节点的值与sum是否相等，如果相等的话，则找到满足条件的一条路径
  10.       const flag = (cRoot.val === sum) ? 1 : 0
  11.       const cLeft = dfs(cRoot.left, sum - cRoot.val)
  12.       const cRight = dfs(cRoot.right, sum - cRoot.val)
  13.       return flag + cLeft + cRight
  14.     }
  15.     const page = dfs(root, targetSum) // 以当前节点为起点，满足条件的个数
  16.     const left = recursion(root.left)
  17.     const right = recursion(root.right)
  18.     return page + left + right
  19.   }
  20.   return recursion(root)
  21. };

拓展：

哈夫曼树

哈夫曼树又称为最优树. 1、路径和路径长度 在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

2、结点的权及带权路径长度 若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

3、树的带权路径长度 树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

树中的前缀和：https://www.cnblogs.com/pjxpjx/p/12388320.html 漫画：什么是 “哈夫曼树”？