题目

题目来源：力扣（LeetCode）

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：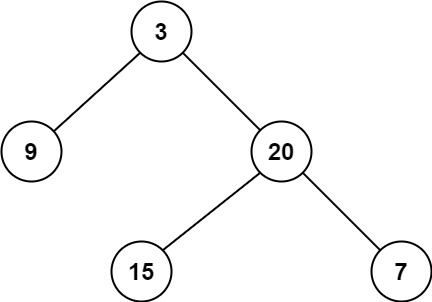
image.png

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

思路分析

深度优先搜索

  1. 使用深度优先搜索的方法，遍历整棵树，记录最小深度。
  2. 对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。
  3. 当前节点root 为空的时候，说明此树的深度度为0，0也是最小值
  4. 当前节点root的左子树和右子树都不为空的时候，则说明当前节点有值，且需要分别计算其左子树和右子树的最小深度，返回最小深度 +1，+1表示当前节点存在有1个深度。
  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} root
  11.  * @return {number}
  12.  */
  13. var minDepth = function (root) {
  14.   // 当前节点root 为 null 的时候，说明此树的深度为0，0也是最小值
  15.   if (root == null) {
  16.     return 0;
  17.   }
  18.   // 左右子树都不存在，当前节点的深度1
  19.   if (root.left == null && root.right == null) {
  20.     return 1;
  21.   }
  22.   // 当前子树的深度
  23.   let ans = Number.MAX_SAFE_INTEGER;
  24.   // 左子树存在，右子树不存在
  25.   if (root.left != null) {
  26.     // 求出左子树的深度，取两者的最小值
  27.     ans = Math.min(minDepth(root.left), ans);
  28.   }
  29.   // 右子树存在，左子树不存在
  30.   if (root.right != null) {
  31.     // 求出右子树的深度，取两者的最小值
  32.     ans = Math.min(minDepth(root.right), ans);
  33.   }
  34.   // 最后返回最小深度 + 1 ， + 1 表示当前节点存在有 1 个深度
  35.   return ans + 1;
  36. };

广度优先搜索

  1. 使用广度优先搜索的方法，遍历整棵树。
  2. 当我们找到一个叶子节点时，直接返回这个叶子节点的深度。广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小。
  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} root
  11.  * @return {number}
  12.  */
  13. const minDepth = (root) => {
  14.   if (root == null) return 0;
  15.   // 根节点入列
  16.   const queue = [root];
  17.   // 当前层的深度
  18.   let depth = 1;
  20.   while (queue.length) { // 直到清空队列
  21.     const levelSize = queue.length; // 当前层的节点个数
  22.     for (let i = 0; i < levelSize; i++) { // 遍历 逐个出列
  23.       const cur = queue.shift();  // 出列
  24.       if (cur.left == null && cur.right == null) { // 如果没有孩子，直接返回所在层数
  25.         return depth;
  26.       }
  27.       // 有左孩子，让左孩子入列
  28.       if (cur.left) queue.push(cur.left); 
  29.       // 有右孩子，让右孩子入列
  30.       if (cur.right) queue.push(cur.right);
  31.     }
  32.     depth++; // 肯定有下一层，继续遍历下一层
  33.   }
  34. };