题目

题目来源：力扣（LeetCode）

在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。
输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：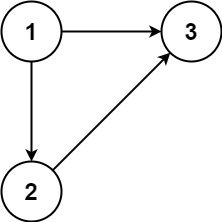
image.png

输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

示例 2：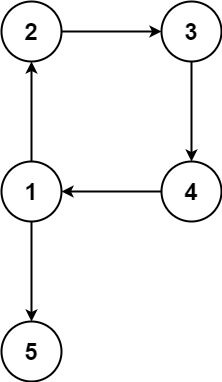
image.png

输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

思路分析

什么是有根树

题目中，给出了有根树的定义：

有根树是值满足以下条件的 有向图：该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

由此，我们可以归纳出，有根树的特点：

  • 只有唯一的一个入度为 0 的节点，它是根节点；
  • 不是根节点的其它所有节点入度为 1；
  • 不可能存在入度为 2 的节点

题目分析

在一棵树中，边的数量比节点的数量少 1。如果一棵树有 N 个节点，则这棵树有 N−1 条边。这道题中的图在树的基础上多了一条附加的边，因此边的数量也是 N。

根据有根树的定义，树中的每个节点都有一个父节点，除了根节点没有父节点。在多了一条附加的边之后，可能有以下两种情况：

  • 附加的边指向非根节点，则恰好有一个节点（即被附加的边指向的节点）有两个父节点，此时图中可能有环路也可能没有环路。即示例 1 的情形：

  • 附加的边指向根节点，则包括根节点在内的每个节点都有一个父节点，此时图中一定有环路。即示例2的情形：

要找到附加的边，需要遍历图中的所有边构建出一棵树，在构建树的构成中寻找导致冲突 (即导致一个节点有两个父节点) 的边以及导致环路出现的边。

具体做法是，使用数组 parent 记录每个节点的父节点，初始时对于任何 1 ≤ i ≤ N 都有 parent[i] = i，另外创建并查集，初始时并查集中的每个节点都是一个连通分支，该连通分支的根节点就是该节点本身。遍历每条边的过程中，维护导致一个节点有两个父节点的边和导致环路出现的边，由于只有一条附加的边，因此最多有一条导致一个节点有两个父节点的边和一条导致环路出现的边。

当访问到边 [u, v] 时，进行如下操作：

如果此时已经有 parent[v] ≠ v ，说明 v 有两个父节点，将当前的边 [u,v] 记为导致一个节点有两个父节点的边；

否则，令 parent[v] = u，然后在并查集中分别找到 u 和 v 的祖先（即各自的连通分支中的根节点），如果祖先相同，说明这条边导致环路出现，将当前的边 [u, v] 记为导致环路出现的边，如果祖先不同，则在并查集中将 u 和 v 进行合并。

根据上述操作，同一条边不可能同时被记为导致一个节点有两个父节点的边和导致环路出现的边。如果访问到的边确实同时导致一个节点有两个父节点和环路出现，则这条边被记为导致一个节点有两个父节点的边。

在遍历图中的所有边之后，根据是否存在导致一个节点有两个父节点的边和导致环路出现的边，得到附加的边。

如果没有导致一个节点有两个父节点的边，说明附加的边一定导致环路出现，而且是在环路中的最后一条被访问到的边，因此附加的边即为导致环路出现的边。

如果有导致一个节点有两个父节点的边，记这条边为 [u,v]，则有两条边指向 v，另一条边为[parent[v],v]，需要通过判断是否有导致环路的边决定哪条边是附加的边。

如果有导致环路的边，则附加的边不可能是 [u,v]（因为[u,v] 已经被记为导致一个节点有两个父节点的边，不可能被记为导致环路出现的边），因此附加的边是[parent[v],v]。

如果没有导致环路的边，则附加的边是后被访问到的指向 v 的边，因此附加的边是 [u,v]。

  1. /**
  2.  * @param {number[][]} edges
  3.  * @return {number[]}
  4.  */
  5. let findRedundantDirectedConnection = (edges) => {
  6.   // 获取边的数量，题目中的图在树的基础上多了一条附加的边，因此边的数量也是节点的数量
  7.   let nodeCount = edges.length;
  8.   // 根据节点的个数构建并查集，加 1 是避免它从 0 开始
  9.   let uf = new UnionFind(nodeCount + 1);
  10.   // 数组parent用于记录每个节点的父节点
  11.   let parent = [];
  12.   // 初始时，每个节点的根节点都是自身
  13.   for (let i = 1; i <= (nodeCount + 1); i++) {//遍历边的长度加1
  14.     parent[i] = i; //做一个初始化
  15.   }
  16.   // 用来记录是否产生了双重父节点的情况
  17.   let conflict = - 1;
  18.   // 用来记录是否产生了环路
  19.   let cycle = -1;
  20.   for (i in edges) {
  21.     let edge = edges[i]
  22.     let node1 = edge[0], node2 = edge[1];//拿到两个节点
  23.     if (parent[node2] != node2) { //node2这个节点有两个父节点
  24.       conflict = i;// 当前的边为导致一个节点有两个父节点的边，将其记录下来
  25.     } else { //否则就是没有父节点，就把他们连起来
  26.       parent[node2] = node1;
  27.       // 在并查集中查找 node1 和 node2 的根节点，如果根节点相同，说明这条边导致环路出现
  28.       if (uf.findSet(node1) == uf.findSet(node2)) { // 产生环路
  29.         // 将导致环路出现的边记录下来
  30.         cycle = i;
  31.       } else {
  32.         // 根节点不同，在并查集中将两个节点进行合并
  33.         uf.unite(node1, node2); //两种情况都没有，就给他们连起来
  34.       }
  35.     }
  36.   }
  37.   if (conflict < 0) {
  38.     // 没有导致双重父节点产生，说明附加的边一定导致环路出现，那么附加的边为导致环路出现的边
  39.     return edges[cycle];
  40.   } else { // 有双重父节点产生
  41.     let conflictEdge = edges[conflict];
  43.     if (cycle >= 0) {
  44.       // 有导致环路出现的边，附加的边为 [parent[v], v]
  45.       return [parent[conflictEdge[1]], conflictEdge[1]]
  46.     } else {
  47.       // 没有导致环路出现，附加的边是 [u, v]
  48.       return conflictEdge;
  49.     }
  50.   }
  51. }
  53. // 并查集
  54. class UnionFind {
  55.   constructor(n) {
  56.     // 元素所指向的父节点，parent[i] 表示第 i 个元素所指向的父节点
  57.     // 初始化时, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
  58.     this.parent = new Array(n).fill(0).map((value, index) => index);
  59.     // 树的层数，rank[i] 表示以 i 为根的集合所表示的树的层数
  60.     this.rank = new Array(n).fill(1);
  61.     // 节点的个数
  62.     this.setCount = n;
  63.   }
  65.   // 查找过程，查找元素 index 所在集合的编号(查找树的根节点)
  66.   findSet(index) {
  67.     // 不断去查询自己的父节点，直至根节点
  68.     // 根节点的标志是父节点就是本身  parent[index] == index
  69.     if (this.parent[index] != index) {
  70.       // 递归获取节点的父节点
  71.       this.parent[index] = this.findSet(this.parent[index]);
  72.     }
  73.     // 返回根节点
  74.     return this.parent[index];
  75.   }
  77.   // 合并两个集合
  78.   unite(index1, index2) {
  79.     let root1 = this.findSet(index1);
  80.     let root2 = this.findSet(index2);
  81.     // 根节点不一样，是两个不同的集合(两棵不同的树)
  82.     if (root1 != root2) {
  83.       // 根据树的层数合并集合
  84.       // 
  85.       if (this.rank[root1] < this.rank[root2]) {
  86.         // 这个判断如果 root2 所在树的层数 大于 root1，就交换两个父节点，这样始终让 root1 为父节点
  87.         [root1, root2] = [root2, root1];
  88.       }
  89.       // 将层数多的集合合并到集合少的集合
  90.       this.parent[root2] = root1;
  91.       this.rank[root1] += this.rank[root2];
  92.       this.setCount--;
  93.     }
  94.   }
  96.   getCount() {
  97.     return this.setCount;
  98.   }
  100.   connected(index1, index2) {
  101.     return this.findSet(index1) === this.findSet(index2);
  102.   }
  103. }