验证二叉搜索树

题目

题目来源：力扣（LeetCode）

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：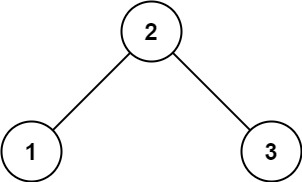

输入：root = [2,1,3]
输出：true

示例 2：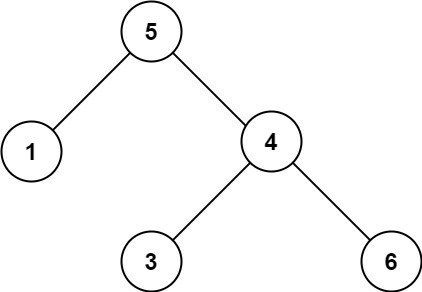

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路分析

若一棵二叉树为二叉搜索树，则有以下性质：

1. 若任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不为空，则右子树上所有子节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉搜索树；

二叉搜索树的中序遍历顺序为: 左子树 -> 根节点 -> 右子树

结合二叉搜索树的性质，可得：二叉搜索树的中序遍历结果是一个升序序列。

因此，我们可以在中序遍历时，判断当前节点的值是否大于中序遍历的前一个节点的值，如果均大于说明这个序列是升序的，整棵树是二叉搜索树，否则不是，那么就返回false。

递归实现中序遍历

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  let pre = -Infinity
  return inOrder(root,)
  function inOrder(root) {
    if (root == null) {
      return true;
    }
    // 访问左子树
    if (!inOrder(root.left)) {
      return false;
    }
    // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；否则继续遍历。
    if (root.val <= pre) {
      return false;
    }
    pre = root.val;
    // 访问右子树
    return inOrder(root.right);
  }
}

栈模拟中序遍历

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  let stack = [];
  let inorder = -Infinity;
  while (stack.length || root !== null) {
    while (root !== null) {
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
    if (root.val <= inorder) {
      return false;
    }
    inorder = root.val;
    root = root.right;
  }
  return true;
};