题目

题目来源：力扣（LeetCode）

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：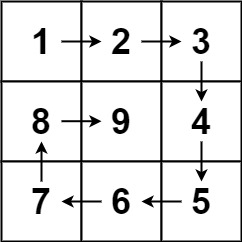
image.png

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

思路分析

1、构建 n * n 的矩阵，确定矩阵的四个边界，它是初始遍历的边界。
2、模拟顺时针画矩阵的过程，按照上、右、下、左的顺序填充：
（1）填充上行从左到右
（2）填充右列从上到下
（3）填充下行从右到左
（4）填充左列从下到上。
3、每遍历一个格子，填上对应的 count，count自增。
4、每次填充完一圈后，更新起点位置
5、最后判断 n 是否是奇数，若是奇数，中间格子需要单独填充

  1. /**
  2.  * @param {number} n
  3.  * @return {number[][]}
  4.  */
  5. var generateMatrix = function (n) {
  6.   // new Array(n).fill(new Array(n))
  7.   // 使用fill --> 填充的是同一个数组地址
  8.   const res = Array.from({ length: n }).map(() => new Array(n));
  9.   // 填充一圈为一个循环
  10.   let loop = n >> 1,  // 循环次数
  11.     i = 0, // 当前是第几次循环
  12.     count = 1, // 要填充的数字
  13.     startX = startY = 0; // 每次循环的起始位置
  14.   while (++i <= loop) {
  15.     // 定义行列初始位置
  16.     let row = startX, column = startY;
  17.     // [ startY, n - i) 填充左到右
  18.     // 上：行不动，列增加
  19.     while (column < n - i) {
  20.       res[row][column++] = count++;
  21.     }
  23.     // [ startX, n - i) 填充上到下
  24.     // 右：列不动，行增加
  25.     while (row < n - i) {
  26.       res[row++][column] = count++;
  27.     }
  29.     // [n - i , startY) 填充右到左
  30.     // 下：行不动，列减少
  31.     while (column > startY) {
  32.       res[row][column--] = count++;
  33.     }
  35.     // [n - i , startX) 填充下到上
  36.     // 左：列不动，行减少
  37.     while (row > startX) {
  38.       res[row--][column] = count++;
  39.     }
  41.     // 循环一次后，更新循环的起点位置
  42.     startX = ++startY;
  43.   }
  44.   // 若果 n 是奇数，则中间的各自需要单独填充
  45.   if (n & 1) {
  46.     res[startX][startY] = count;
  47.   }
  48.   return res;
  49. };