归并排序

归并排序 (Merge sort) 是建立在归并操作上的一种有效的排序算法，该算法是采用分治法 (Divide and Conquer) 的一个非常典型的应用。归并排序是一种稳定的排序算法。它将已有序的子序列合并，得到完全有序的序列。

作为一种典型的分而治之思想的算法应用，归并排序的实现有两种方法：

• 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第二种方法）；
• 自下而上的递归；

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度，代价是需要额外的内存空间。

时间复杂度

• 最佳情况：T(n) = O(n)
• 最差情况：T(n) = O(nlogn)
• 平均情况：T(n) = O(nlogn)

实现思路

1. 把长度为 n 的输入序列分成两个长度为 n/2 的子序列；
2. 对这两个子序列分别采用归并排序；
3. 将两个排序好的子序列合并成一个最终的排序序列；

实现步骤

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3. 比较两个指针指向的元素，选择相对小的元素放入到合并空间中，并移动指针到下一位置；
4. 重复 步骤3 直到某一指针达到序列尾；
5. 将另一序列剩下的所有元素直接合并到序列尾

动图演示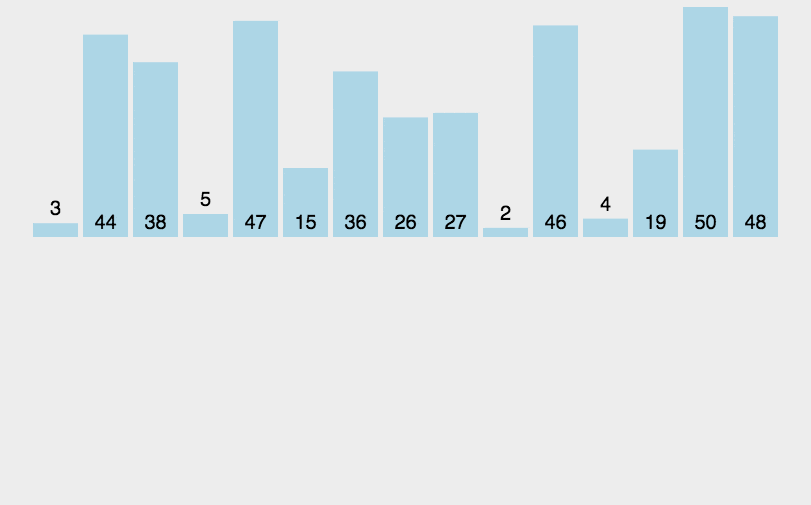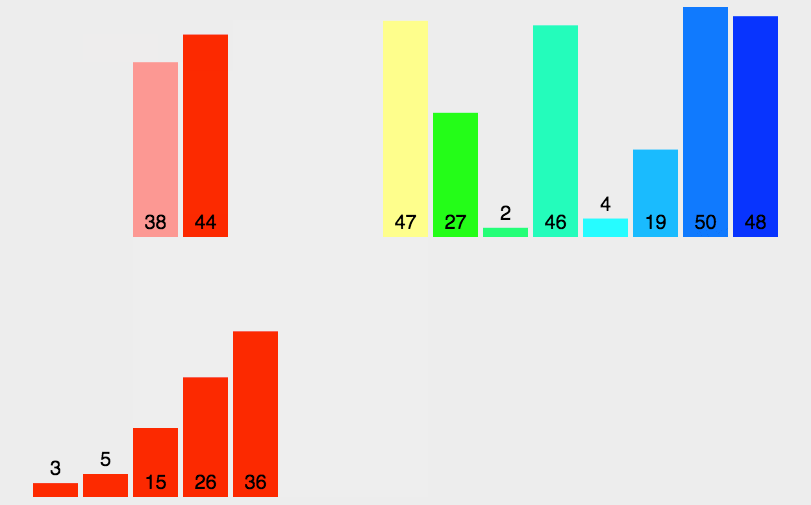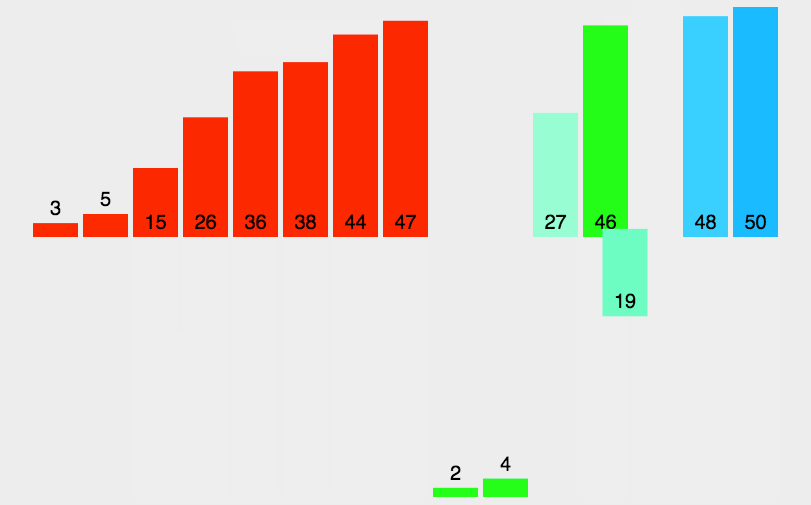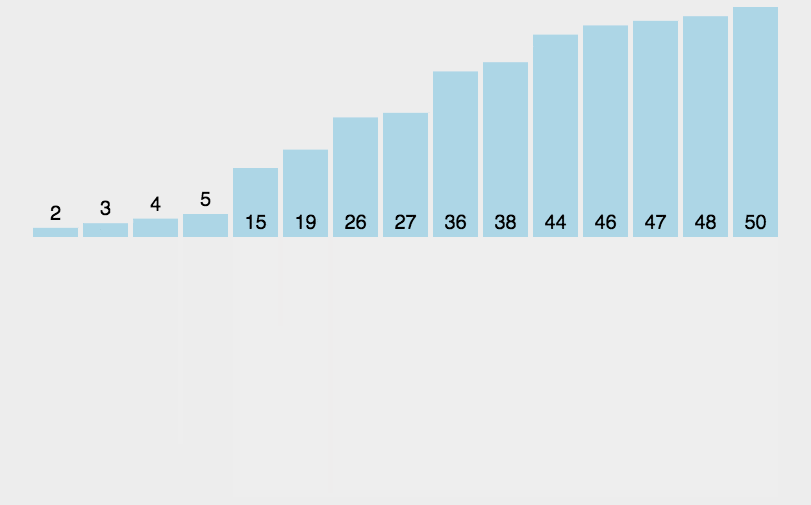

JavaScript 代码实现

function mergeSort(arr) { // 采用自上而下的递归方法
    const len = arr.length;
  if (len < 2) {
      return arr;
  }
  const middle = Math.floor(len / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);
  return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
    const result = [];
  while(left.length && right.length) {
      if (left[0] <= right[0]) {
        result.push(left.shift());
    } else {
        result.push(right.shift());
    }
  }
  while(left.length) {
      result.push(left.shift());
  }
  while(right.length) {
      result.push(right.shift());
  }
  return result;
}