题目

题目来源：力扣（LeetCode）

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构（即，如果没有被移除，原有的父代子代关系都应当保留）。 可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：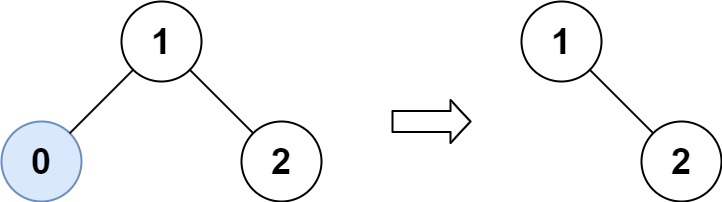
image.png
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：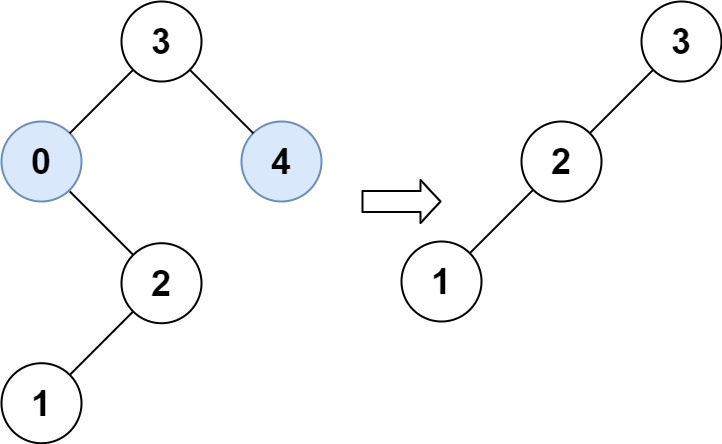
image.png
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

示例 3：

输入：root = [1], low = 1, high = 2
输出：[1]

示例 4：

输入：root = [1,null,2], low = 1, high = 3
输出：[1,null,2]

示例 5：

输入：root = [1,null,2], low = 2, high = 4
输出：[2]

思路分析

方法一：迭代

以下面的二叉搜索树为例：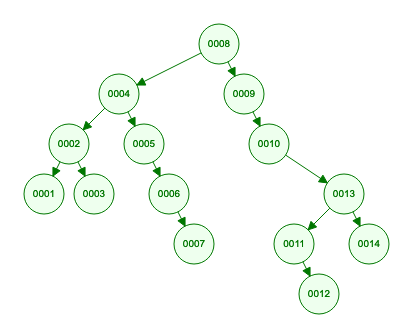
image.png
当要取的区间是：[11， 14]，那么从节点 8 开始做剪枝肯定是不合适的。

所以第一步是找到第一个满足 [low, high] 区间的子节点，以该子节点为根节点，开始做剪枝逻辑。
以第一步为起点，分别做向下遍历：

  • 在遍历左树时，如果遇到 root.val < low 就直接把 root 节点的父节点的 left指针 指向root节点的right指针
  • 在遍历右树时，如果遇到 root.val > high 就直接把 root节点的父节点的 right指针 指向root节点的left指针
  • 最后返回root指针
  1. var trimBST = function (root, low, high) {
  2.   if (root === null) {
  3.     return null;
  4.   }
  5.   // 处理头节点，让 root 移动到 [low, high] 范围内，注意是左闭右闭
  6.   while (root !== null && (root.val < low || root.val > high)) {
  7.     // 如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
  8.     if (root.val < low) {
  9.       root = root.right;
  10.     }
  11.     // 如果该节点的值大于最大值，则该节点更换为该节点的左节点值，继续遍历
  12.     else {
  13.       root = root.left;
  14.     }
  15.   }
  16.   let cur = root;
  17.   // 此时root已经在[low, high] 范围内，处理左孩子元素小于 low 的情况
  18.   while (cur !== null) {
  19.     // 如果左孩子小于 low ，则将左孩子替换为左孩子的右子节点
  20.     while (cur.left && cur.left.val < low) {
  21.       cur.left = cur.left.right;
  22.     }
  23.     cur = cur.left;
  24.   }
  25.   cur = root;
  26.   // 此时 root 已经在[low, high] 范围内，处理右孩子大于 high 的情况
  27.   while (cur !== null) {
  28.     // 如果右孩子大于 high，则将右孩子替换为右孩子的左子节点
  29.     while (cur.right && cur.right.val > high) {
  30.       cur.right = cur.right.left;
  31.     }
  32.     cur = cur.right;
  33.   }
  34.   return root;
  35. };

方法二：递归

二叉搜索树的特点是：根节点值大于它的左子节点并且大于它的右子节点

  1. 如果节点值 < low，那么把它的左子树剪掉，继续修剪它的右子树
  2. 如果节点值 > high，那么把它的右子树剪掉，继续修剪它的左子树
  3. 如果当前节点值在 [low, high] 双闭区间内，那么它的左右子树都有可能仍然有符合条件的节点值，所以需要继续修剪左右子树：
    • 如果是在双闭区间什么也不改动，继续向下遍历
    • 如果不是，当该节点小余当前节点时，说明该节点就我们要剪枝的节点，返回该节点的右节点(右节点 > 当前节点)，如图，也就是 5
    • 如果不是，当该节点大余当前节点时，说明该节点就我们要剪枝的节点，返回该节点的左节点(左节点 < 当前节点)，如图，也就是 11

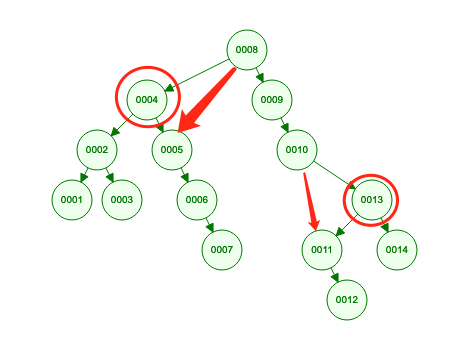
image.png
在这颗二叉搜索树中，只取双闭区间：[5, 12] 内的数。

当遇到节点值为 4 的节点，那么把它的父节点(8)的 left 指针 指向 节点4的 right指针
当遇到节点值为 13 的节点，那么把它的父节点(10)的 right 指针 指向 节点13的 left指针

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val, left, right) {
  4.  *     this.val = (val===undefined ? 0 : val)
  5.  *     this.left = (left===undefined ? null : left)
  6.  *     this.right = (right===undefined ? null : right)
  7.  * }
  8.  */
  9. /**
  10.  * @param {TreeNode} root
  11.  * @param {number} low
  12.  * @param {number} high
  13.  * @return {TreeNode}
  14.  */
  15. var trimBST = function (root, low, high) {
  16.   if (root === null) {
  17.     return null;
  18.   }
  19.   // 如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
  20.   if (root.val < low) {
  21.     let right = trimBST(root.right, low, high);
  22.     return right;
  23.   }
  24.   // 如果该节点的值大于最大值，则该节点更换为该节点的左节点值，继续遍历
  25.   if (root.val > high) {
  26.     let left = trimBST(root.left, low, high);
  27.     return left;
  28.   }
  29.   // 继续修剪左右子树
  30.   root.left = trimBST(root.left, low, high);
  31.   root.right = trimBST(root.right, low, high);
  32.   return root;
  33. }

参考： https://leetcode-cn.com/problems/trim-a-binary-search-tree/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-er-ch-mebi/ https://leetcode-cn.com/problems/trim-a-binary-search-tree/solution/2chong-jie-fa-cji-jian-dai-ma-by-fengzil-mj8q/