栈的定义
栈是一种遵从 后进先出(LIFO)原则的有序集合。新添加或待删除的元素都保存在栈的同一端,称作栈顶,另一端就叫栈底。在栈里,新元素都靠近栈顶,旧元素都接近栈底。如图: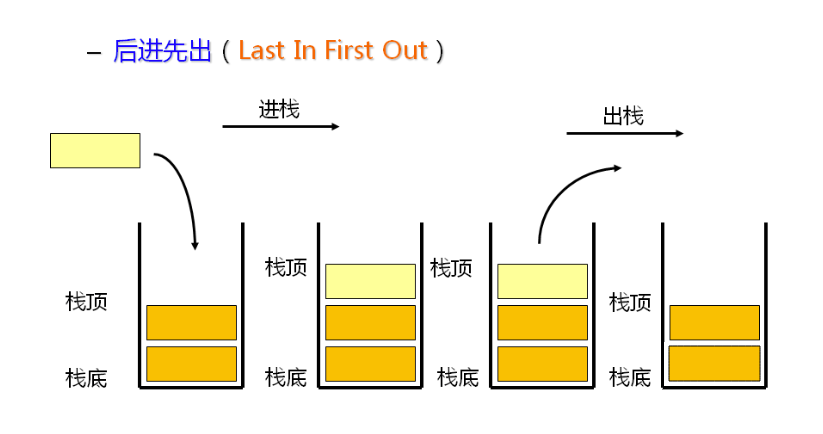
基于数组的栈
我们使用 ES6 的类来创建一个基于数组的栈:
class Stack {constructor() {this.items = []}}
接下来,为栈声明一些方法:
push(element):添加一个或多个新元素到栈顶
pop():移除栈顶的元素,同时返回被移除的元素
peek():查看栈顶的元素,不对栈做任何修改
isEmpty():判断栈是否为空,如果栈里没有任何元素就返回 true,否则返回 false
clear():清空栈,即移除栈里的所有元素
size(): 返回栈里的元素个数,该方法和数组的 length 属性类似
print(): 打印栈元素,将栈中的元素以字符串的形式打印出来
下面,我们逐一实现栈的方法:
push 向栈添加元素
push 方法负责往栈里添加新元素,该方法只能添加元素到栈顶
// 往栈里压入一个元素,因为使用数组实现栈,往栈里压入元素就是往数组的末尾添加元素push(element) {this.items.push(element);}
pop 从栈顶移除元素
pop 方法用来移除栈顶的元素,也就是移除的是最后添加进去的元素
// 移除栈顶元素,因为使用数组实现栈,移除栈顶元素就是移除数组的最后一个元素pop() {return this.items.pop();}
peek 查看栈顶元素
peek() {return this.items[this.items.length - 1]}
isEmpty 检查栈是否为空
isEmpty 方法检查栈是否为空,如果栈为空就返回 true,否则就放回 false
isEmpty() {return this.items.length === 0;}
clear 清空栈
clear 方法用来移除栈里所有的元素,把栈清空
clear() {this.items = []}
size 返回栈里的元素个数
size() {return this.items.length}
print 打印栈元素
print() {return this.items.toString();}
完整代码
class Stack {constructor() {this.items = [];}push(element) {this.items.push(element);}pop() {return this.items.pop();}peek() {return this.items[this.items.length - 1];}isEmpty() {return this.items.length === 0;}clear() {this.items = [];}size() {return this.items.length;}print() {return this.items.toString()}}
基于对象的栈
除了可以使用数组来实现栈,也可以使用JavaScript对象来存储所有的栈元素,保证它们的顺序并且遵循 LIFO 原则。在使用对象实现是栈中,使用 count 变量来记录栈元素的个数,并且使用 count 变量作为键将栈元素存储在 items 对象中。
class Stack {constructor() {// 栈的个数this.count = 0;// 存储栈元素this.items = {};}}
push 向栈插入元素
我们将 count 作为键,插入的元素作为值存储在对象中
push(element) {this.items[this.count] = element;this.count++;}
pop 从栈顶移除元素
pop() {// 栈是否为空,为空则返回 undefinedif (this.isEmpty()) {return undefined;}// count 属性减 1,此时的值即为栈顶元素在对象中的位置this.count--;// 根据 count 取出栈顶元素const result = this.items[this.count];// 删除栈顶元素delete this.items[this.count];// 将栈顶元素返回return result;}
peek 查看栈顶元素
peek() {if (this.isEmpty()) {return undefined;}// count 属性 减 1 后的值即为 栈顶元素的健值return this.items[this.count - 1];}
isEmpty 检查栈是否为空
isEmpty() {// count 变量表示栈的元素个数return this.count === 0;}
clear 清空栈
清空栈,只需将 items变量复原为空对象,count 变量复原为 0 即可
clear() {// 将对象置为空对象this.items = {};// 将 count 变量置为 0this.count = 0;}
size 返回栈里的元素个数
size() {return this.count;}
print 打印栈元素
print() {// 栈为空,返回空字符串if (this.isEmpty) {return '';}let objString = `${this.items[0]}`;// 迭代 栈的键,一直到栈顶,将栈元素拼接成字符串for (let i = 1; i <this.count; i++) {objString = `${objString},${this.items[i]}`;}return objString;}
完整代码
class Stack {constructor() {// 栈的个数this.count = 0;// 存储栈元素this.items = {};}push(element) {this.items[this.count] = element;this.count++;}pop() {// 栈是否为空,为空则返回 undefinedif (this.isEmpty()) {return undefined;}// count 属性减 1,此时的值即为栈顶元素在对象中的位置this.count--;// 根据 count 取出栈顶元素const result = this.items[this.count];// 删除栈顶元素delete this.items[this.count];// 将栈顶元素返回return result;}peek() {if (this.isEmpty()) {return undefined;}// count 属性 减 1 后的值即为栈顶元素的健值return this.items[this.count - 1];}isEmpty() {// count 变量表示栈的元素个数return this.count === 0;}clear() {// 将对象置为空对象this.items = {};// 将 count 变量置为 0this.count = 0;}size() {return this.count;}print() {// 栈为空,返回空字符串if (this.isEmpty()) {return '';}let objString = `${this.items[0]}`;// 迭代 栈的键,一直到栈顶,将栈元素拼接成字符串for (let i = 0; i < this.count; i++) {objString = `${objString}, ${this.items[i]}`;}return objString;}}
栈的应用
进制转换
在现实生活中,我们主要使用十进制,但在计算科学中,计算机里的所有内容都是用二进制数字表示的 (0 和 1)。要与计算机节流,就必须把十进制转换成二进制。
要把十进制转换成二进制,我们可以将十进制数除以 2,并对商取整,直到商为 0 为止。举个例子,把十进制的数 20 转换成二进制的数字,其过程如下: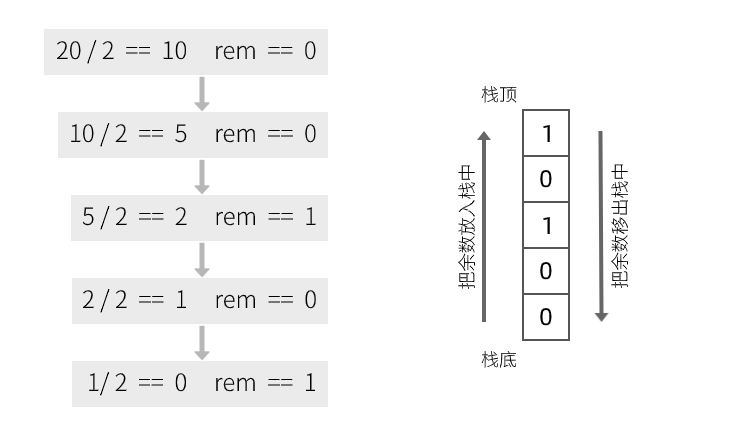
思路分析:
将十进制数除以 2,当除法的结果 (商) 不为 0 时,我们会获得一个余数,并将余数放到栈里
然后让结果 (商) 继续除以 2,并将余数入栈,直到结果 (商) 为 0
将栈中的元素出栈,连接成字符串,就是转换后的二进制数,如上图,转换后的二进制位 10100
代码实现
const decimalToBinary = (decNumber) => {const stack = new Stack();let number = decNumber;let remainder;let binaryNumber = '';while (number > 0) {// 获取余数remainder = Math.floor(number % 2);// 将余数入栈stack.push(remainder);// 将结果 (商) 除以 2number = Math.floor(number / 2);}while (!stack.isEmpty()) {// 栈元素出栈,拼接成字符串binaryNumber += stack.pop().toString();}return binaryNumber}console.log(decimalToBinary(20)) // 10100console.log(decimalToBinary(10)) // 1010console.log(decimalToBinary(1000)) // 1111101000console.log(decimalToBinary(255)) // 11111111
下面,我们将十进制转二进制的算法进行改造,使之能把十进制转换成基数为 2~36 的任意进制。除了把十进制数除以 2 转成 二进制数,还可以传入其他任意进制的基数为参数,然后转换成相应的进制数。
const baseConverter = (decNumber, base) => {const stack = new Stack();const digits = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ';let number = decNumber;let remainder;let baseString = '';if (!(base >=2 && base <=36)) {return '';}while(number > 0) {remainder = Math.floor(number % base);stack.push(remainder);number = Math.floor(number / base);}while(!stack.isEmpty()) {baseString += digits[stack.pop()];}return baseString;}
合法括号
下面的字符串中包含小括号,编写一个函数判断字符串中的括号是否合法,所谓合法,就是括号成对出现
sdf(ds(ew(we)rw)rwqq)qwewe 合法(sd(qwqw)sd(sd)) 合法()()sd()(sd()fw))( 不合法
思路分析:**
括号存在嵌套关系,也存在并列关系,如果使用数组存储这些括号,然后再一对一对的将括号抵消掉,这似乎是一个可行的办法,可是如何判断一个左括号对应的是哪个右括号呢?在使用数组的角度上思考这个问题,就会陷入一种无从下手的绝望之中。
我们换个思路,在栈的角度上思考这个问题,解题的步骤就非常简单。我们可以使用 for 循环遍历字符串中的每个字符,对每个字符做如下的操作:
- 遇到左括号,就把左括号压入栈中
- 遇到右括号,判断栈是否为空,为空则说明没有左括号与之对应,缺少左括号,字符串括号不合法;如果栈不为空,则把栈顶元素移除,这对括号就抵消掉了
当 for 循环结束之后,如果栈是空的,就说明所有的左右括号都抵消掉了,如果栈里还有元素,则说明缺少右括号,字符串括号不合法
实现代码:
下面,我们使用 栈 解题
const isLeaglBrackets = (str) => {const stack = new Stack();for (let i = 0; i < str.length; i++) {const item = str[i];if (item === '(') {// 将 左括号 压入 栈stack.push(item);} else if (item === ')') {// 如果为空,就说明没有左括号与右括号抵消if (stack.isEmpty()) {return false;} else {// 将左括号弹出栈stack.pop();}}}// 栈是否为空,为空则说明字符串中所有的左右括号都抵消掉了,那么字符串中的括号是合法的,否则是不合法的return stack.size() === 0;}console.log(isLeaglBrackets("()()))")); // falseconsole.log(isLeaglBrackets("sdf(ds(ew(we)rw)rwqq)qwewe")); // trueconsole.log(isLeaglBrackets("()()sd()(sd()fw))(")); // false
计算逆波兰表达式
逆波兰表达式,也叫后缀表达式,它将复杂表达式转换为可以依靠简单的操作得到计算结果的表达式,例如我们平时写 a + b,这是中缀表达式,写成后缀表达式就是: ab+。又比如中缀表达式 (a+b)*c 写成后缀表达式为:ab+c*
现在我们实现一个算法,来计算逆波兰表达式
["4", "13", "5", "/", "+"] 等价于(4 + (13 / 5)) = 6["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"] 等价于((10 *(6 / ((9 + 3) * -11))) + 17) + 5
思路分析:
**
[‘4’, ‘13’, ‘5’, ‘/‘, ‘+’] 是一个数组,我们在数组的角度来思考这个问题,遇到 ‘ / ‘ 时,把 13 和 5 从数组里取出来计算,然后把 13 和 5 删除并不计算结果放入到数组中 4 的后面。天哪,太复杂了,太笨拙了,我已经无法继续思考了😱
如果是使用栈来解决这个问题,一切就那么的简单而自然,使用 for 循环遍历数组,对每一个元素做如下操作:
- 如果元素不是
+ - * /中的某一个,就压入栈中 - 如果元素是
+ - * /中的某一个,则从栈里连续弹出两个元素,并对这两个元素进行计算,将计算结果压入栈中
for 循环结束之后,栈里只有一个元素,这个元素就是整个表达式的计算结果
实现代码
const cacl_inverse_polish_expression = (exp) => {const stack = new Stack();for (let i = 0; i < exp.length; i++) {const item = exp[i]if (['+', '-', '*', '/'].indexOf(item) >= 0) {// 从栈顶弹出两个元素const value_1 = stack.pop();const value_2 = stack.pop();// 拼成表达式const expStr = value_2 + item + value_1;// 计算结果并取整const result = parseInt(eval(expStr));// 将计算结果压入栈stack.push(result.toString());} else {stack.push(item);}}// 表达式如果是正确的,最终栈里只有一个元素,且就是表达式计算的结果return stack.pop();}const exp_1 = ["4", "13", "5", "/", "+"];const exp_2 = ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"];console.log(cacl_inverse_polish_expression(exp_1)); // 输出结果:6console.log(cacl_inverse_polish_expression(exp_2)); // 输出结果:22
中缀表达式转后缀表达式
中缀表达式是人们常用的算术表示方法,例如 3 + 4、8 + 4 * 6 等都是中缀表达式,操作符以中缀的形式处于操作数中间。
后缀表达式也称作逆波兰表达式,通常是将运算符写在操作数之后,如将中缀表达式 3 + 4 写成后缀表达式就是 34+。
下面,我们实现一个算法,将中缀表达式转换成后缀表达式
输⼊:["12","+", "3"]输出:["12","3","+"]输⼊:["(","1","+","(","4","+","5","+","3",")","-","3",")","+","(","9","+","8",")"]输出:[ '1', '4', '5', '+', '3', '+', '+', '3', '-', '9', '8', '+', '+' ]输⼊:['(', '1', '+', '(', '4', '+', '5', '+', '3', ')', '/', '4', '-', '3', ')', '+', '(', '6', '+', '8', ')', '*', '3']输出:['1', '4', '5', '+', '3', '+', '4', '/', '+', '3', '-', '6', '8', '+', '3', '*', '+']
思路分析:
定义一个数组 postfixList ,用于存储后缀表达式,遍历中缀表达式,对每一个遍历到的元素做如下处理:
如果是数字,直接放入 postfixList 中
- 遇到左括号则入栈
- 遇到右括号,把栈顶元素弹出并放入到 postfixList 中,直到遇到左括号,最后弹出左括号
- 遇到运算符,把栈顶的运算符弹出,直到栈顶的运算符优先级低于当前运算符,把弹出的运算符加入到 postfixList 中,当前的运算符入栈
- for 循环结束后,栈里可能还有元素,都弹出放入到 postfixList 中
实现代码
// 定义运算符的优先级const priorityMap = {"+": 1,"-": 1,"*": 2,"/": 2}const infixExpToPostfixExp = (exp) => {const stack = new Stack();const postfixList = [];for (let i = 0; i < exp.length; i++) {const item = exp[i];if (!isNaN(item)) {// 如果是数字,直接放入到 postfixList 中postfixList.push(item);} else if (item === "(") {// 遇到左括号入栈stack.push(item);} else if (item === ")") {// 遇到右括号,把栈顶元素弹出,直到遇到左括号while(stack.peek() !== "(") {postfixList.push(stack.pop());}// 左括号出栈stack.pop();} else {// 遇到运算符,把栈顶的运算符弹出,直到栈顶的运算符优先级低于当前运算符while(!stack.isEmpty()&& ['+', '-', '*', '/'].indexOf(stack.peek()) >=0&& priorityMap[stack.peek() >= priorityMap[item]]) {// 把弹出的运算符加入到 postfixList 中postfixList.push(stack.pop());}// 当前运算符入栈stack.push(item);}}// for 循环结束后,栈里可能还有元素,都弹出放入到 postfixList 中while(!stack.isEmpty()) {postfixList.push(stack.pop())}return postfixList}// 12+3console.log(infixExpToPostfixExp(["12","+", "3"]))// 2-3+2console.log(infixExpToPostfixExp(["2","-", "3", "+", "2"]))// (1+(4+5+3)-3)+(9+8)var exp = ["(","1","+","(","4","+","5","+","3",")","-","3",")","+","(","9","+","8",")"];console.log(infixExpToPostfixExp(exp))// (1+(4+5+3)/4-3)+(6+8)*3var exp = ['(', '1', '+', '(', '4', '+', '5', '+', '3', ')', '/', '4', '-', '3', ')', '+', '(', '6', '+', '8', ')', '*', '3']console.log(infixExpToPostfixExp(exp))console.log(infixExpToPostfixExp(["12","+", "3","*", "5"]))console.log(infixExpToPostfixExp(["12","*", "3","+", "5"]))
参考资料:
书籍:《JavaScript数据结构与算法》

