题目

题目来源：力扣（LeetCode）

给你一个只包含 ‘(‘ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

输入：s = “(()”
输出：2
解释：最长有效括号子串是 “()”

示例 2：

输入：s = “)()())”
输出：4
解释：最长有效括号子串是 “()()”

示例 3：

输入：s = “”
输出：0

思路分析

解法一：栈

具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」，这样的做法主要是考虑了边界条件的处理，栈里其他元素维护左括号的下标：

  • 对于遇到的每个 ‘(’ ，我们将它的下标放入栈中
  • 对于遇到的每个 ‘)’ ，我们先弹出栈顶元素表示匹配了当前右括号：
    • 如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
    • 如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」

我们从前往后遍历字符串并更新答案即可。

需要注意的是，如果一开始栈为空，第一个字符为左括号的时候我们会将其放入栈中，这样就不满足提及的「最后一个没有被匹配的右括号的下标」，为了保持统一，我们在一开始的时候往栈中放入一个值为 -1 的元素。

图解：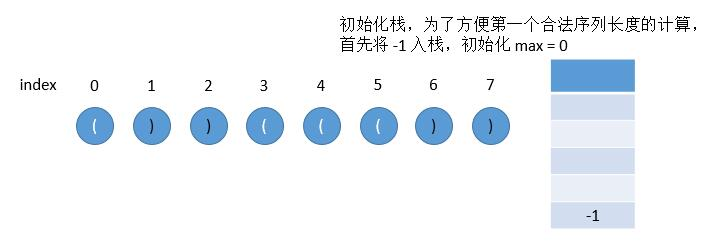
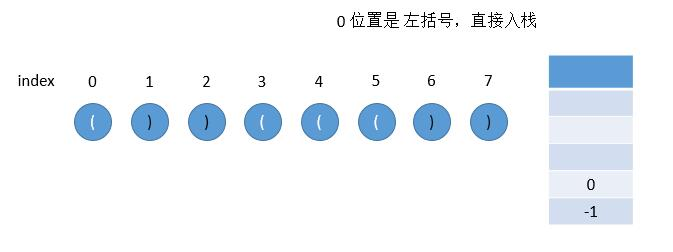
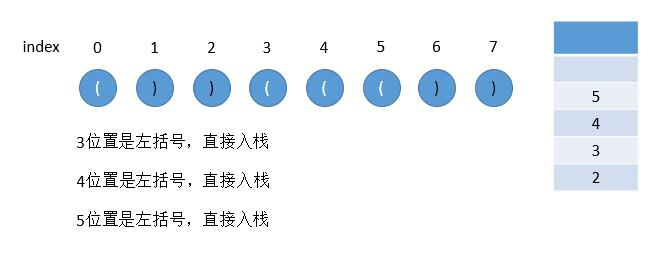
image.png
image.png
image.png
image.png
image.png
image.png
image.png

  1. /**
  2.  * @param {string} s
  3.  * @return {number}
  4.  */
  5. var longestValidParentheses = function (s) {
  6.   let maxans = 0;
  7.   const stack = new Array();
  9.   // 如果一开始栈为空，第一个字符为左括号的时候我们会将其放入栈中，这样就不满足提及的「最后一个没有被匹配的右括号的下标」，
  10.   // 为了保持统一，我们在一开始的时候往栈中放入一个值为 -1−1 的元素
  11.   stack.push(-1);
  12.   for (let i = 0; i < s.length; i++) {
  13.     // 当前遍历到的字符为 '(' ，将它的下标放入栈中
  14.     if (s.charAt(i) == '(') {
  15.       stack.push(i);
  16.     } else {
  17.       // 当前遍历到的字符为 ')' ，弹出栈顶元素表示匹配了当前右括号
  18.       stack.pop();
  19.       if (!stack.length) {
  20.         // 如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中
  21.         stack.push(i);
  22.       } else {
  23.         // 如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
  24.         maxans = Math.max(maxans, i - stack[stack.length - 1]);
  25.       }
  26.     }
  27.   }
  28.   return maxans;
  29. }

解法二：动态规划

1、dp[i]的含义
以当前字符为结尾的 最长有效括号字串的长度

2、dp初始化
有效括号长度肯定是成双成对的，所以dp[0] = 0

3、dp递推公式

  • 如果dp[i] == ‘(‘，那么一个有效括号串，不可能以’(‘结尾，所以如果dp[i] == ‘(‘，dp[i] = 0。

  • 如果dp[i] == ‘)’，此时的情况就有些复杂了，遇到右括号，我们肯定要查找前面有没有和它匹配的左括号，但是这个左括号应该去哪查找呢？我们举一个例子来看。

    • (())

      • 遍历前三个的时候dp[0] = 0, dp[1] = 0, dp[2] = 2，这应该没什么疑问。
      • 当我们遇到最后一个右括号，也就是i = 3的时候，我们应该去哪找跟它匹配的左括号呢？
      • 这时候因为中间两个已经是有效的括号子串了，所以我们要去这个有效子串的前一个的地方也就是 i = 0;的位置找，如果这个地方是’(‘，那么dp[i] = dp[i - 1] + 2;。

    • 完了吗？还没有，我们再看一个例子()(())。

      • 遍历前五个的时候，应该没什么疑问dp[0] = 0, dp[1] = 2, dp[2] = 0, dp[3] = 2, dp[4] = 0。
      • 遍历到最后一个，也就是i = 5的时候，我们又看到了右括号，所以我们去有效子串的前面(即 i = 2的位置)找左括号，找到了，所以(())这四个就是一个有效子串了。
      • 但我们发现，i = 2前面也是一个有效的子串，只不过被这个i = 2给隔开了，现在我们把i = 2这个位置连上了！所以我们还要加上之前dp[i - dp[i - 1] - 2];的子串！

    • 所以完整的递推公式为

      1. if (s[i] === ')') { //只考虑i以‘)’结尾，否则不可能是有效括号
      2. let k = dp[i - 1];
      3. //要想和i-1扯上关系，那么就要看i-1前面那个，也就是 i - k - 1 为下标的s是否存在且对应的是不是'('
      4. if (i - k - 1 >= 0 && s[i - k - 1] === '(') {
      5.  dp[i] = dp[i - 1] + 2; //是的话+2
      6.  //如果前面还存在有效的括号对，直接加进来
      7.  if (i - k - 2 > 0) {
      8.    dp[i] += dp[i - k - 2];
      9.  }
      10. }
      11. }

完整代码：

  1. /**
  2.  * @param {string} s
  3.  * @return {number}
  4.  */
  6. var longestValidParentheses = function (s) {
  7.   let n = s.length;
  8.   let dp = Array(n).fill(0);
  9.   for (let i = 0; i < n; i++) {
  10.     if (s[i] === ')') { //只考虑i以‘)’结尾，否则不可能是有效括号
  11.       let k = dp[i - 1];
  12.       //要想和i-1扯上关系，那么就要看i-1前面那个，也就是 i - k - 1 为下标的s是否存在且对应的是不是'('
  13.       if (i - k - 1 >= 0 && s[i - k - 1] === '(') {
  14.         dp[i] = dp[i - 1] + 2; //是的话+2
  15.         //如果前面还存在有效的括号对，直接加进来
  16.         if (i - k - 2 > 0) {
  17.           dp[i] += dp[i - k - 2];
  18.         }
  19.       }
  20.     }
  21.   }
  22.   return Math.max(...dp, 0)
  23. };

解法三：根据括号的特性

有效括号的特性，就是长度一定是偶数，并且在任何位置左括号的数量都是大于等于右括号的数量的，如果在任何位置右括号大于左括号的数量，那么说明这个组成的括号是无效的。

我们利用两个计数器left 和 right 。首先，我们从左到右遍历字符串，对于遇到的每个 ‘(’，我们增加 eft 计数器，对于遇到的每个 ‘)’ ，我们增加 right 计数器。每当 left 计数器与 right 计数器相等时，我们计算当前有效字符串的长度，并且记录目前为止找到的最长子字符串。当 right 计数器比 left 计数器大时，我们将 left 和 right 计数器同时变回 0。

这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度，每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑，重新从下一个字符开始计算，但这样会漏掉一种情况，就是遍历的时候左括号的数量始终大于右括号的数量，即 (() ，这种时候最长有效括号是求不出来的。

解决的方法也很简单，我们只需要从右往左遍历用类似的方法计算即可，只是这个时候判断条件反了过来：

  • 当 left 计数器比 right 计数器大时，我们将 left 和 right 计数器同时变回 0
  • 当 left 计数器与 right 计数器相等时，我们计算当前有效字符串的长度，并且记录目前为止找到的最长子字符串
  1. /**
  2.  * @param {string} s
  3.  * @return {number}
  4.  */
  6. var longestValidParentheses = function (s) {
  7.   let left = 0, right = 0, max = 0;
  8.   //从前往后右括号大于左括号，left和right都归0
  9.   for (let i = 0; i < s.length; i++) {
  10.     if (s.charAt(i) == '(') {
  11.       left++;
  12.     } else {
  13.       right++;
  14.     }
  15.     //left大于right先不管
  16.     if (left == right) {
  17.       max = Math.max(max, 2 * right);
  18.     } else if (right > left) {
  19.       //right大于left重新记
  20.       left = right = 0;
  21.     }
  22.   }
  23.   left = right = 0;
  24.   //从后往前左括号大于右括号，left和right都归0
  25.   for (let i = s.length - 1; i >= 0; i--) {
  26.     if (s.charAt(i) == '(') {
  27.       left++;
  28.     } else {
  29.       right++;
  30.     }
  31.     if (left == right) {
  32.       max = Math.max(max, 2 * left);
  33.     } else if (left > right) {
  34.       left = right = 0;
  35.     }
  36.   }
  37.   return max;
  38. }

推荐阅读 https://leetcode-cn.com/problems/longest-valid-parentheses/solution/32zui-chang-you-xiao-gua-hao-hua-dong-ch-n5jd/ https://leetcode-cn.com/problems/longest-valid-parentheses/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-7/