题目

题目来源：力扣（LeetCode）

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：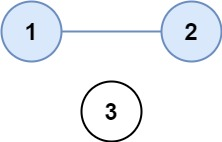
image.png

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：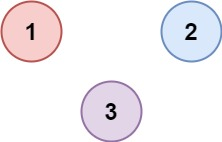
image.png

输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

思路分析

我们来归纳以下题意：n 个城市，有直接/间接相连关系的城市属于同一个省份，求省份的数量。

题意要求我们求省份的数量，可以转化为 求无向图中的连通域的个数，入参 isConnected[i][j] 即为该无向图的邻接矩阵。对图(邻接矩阵是图的一种表示方式)进行遍历，可以使用广度优先搜索进行计数或使用深度优先搜索或者使用并查集。

并查集

初始时，每个城市都属于不同的连同分量，我们初始化 n 个单定点集合，每个集合指向本身，然后遍历城市的邻接矩阵 isConnected，如果两个城市之间有相连关系(直接相连或间接相连)，则它们属于同一个连同分量，对它们进行合并，遍历完邻接矩阵的全部元素之后，计算连同分量的总数，即为省份的总数。

遍历邻接矩阵，也就是遍历图。已知图的顶点数为 n ，则初始化 n 个单定点集合，每个集合指向自身(此时集合中的元素为根节点)，然后遍历图中的每个定点，将当前顶点与其邻接矩点进行合并。最终结果返回合并后的集合的数量即可。

  1. var findCircleNum = function (isConnected) {
  2.   // 初始时城市的数量(连通分量)
  3.     let circleNum = isConnected.length;
  4.   // 根据城市的数量初始化一个并查集
  5.      let uf = new UnionFind(circleNum);
  7.   // 遍历每个定点，将当前定点与其邻接点进行合并
  8.   for (let i = 0; i < circleNum; i++) {
  9.       for (let j = i + 1; j < circleNum; j++) {
  10.         if (isConnected[i][j] == 1) {
  11.           uf.unite(i, j);
  12.       }
  13.     }
  14.   }
  15.   // 返回最终合并后集合的元素个数
  16.   return uf.getCount();
  17. }
  20. // 并查集
  21. class UnionFind {
  22.   constructor(n) {
  23.     // 元素所指向的父节点，parent[i] 表示第 i 个元素所指向的父节点
  24.     // 初始化时, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
  25.     this.parent = new Array(n).fill(0).map((value, index) => index);
  26.     // 树的层数，rank[i] 表示以 i 为根的集合所表示的树的层数
  27.     this.rank = new Array(n).fill(1);
  28.     // 节点的个数
  29.     this.setCount = n;
  30.   }
  32.   // 查找过程，查找元素 index 所在集合的编号(查找树的根节点)
  33.   findSet(index) {
  34.     // 不断去查询自己的父节点，直至根节点
  35.     // 根节点的标志是父节点就是本身  parent[index] == index
  36.     if (this.parent[index] != index) {
  37.       // 递归获取节点的父节点
  38.       this.parent[index] = this.findSet(this.parent[index]);
  39.     }
  40.     // 返回根节点
  41.     return this.parent[index];
  42.   }
  44.   // 合并两个集合
  45.   unite(index1, index2) {
  46.     let root1 = this.findSet(index1);
  47.     let root2 = this.findSet(index2);
  48.     // 根节点不一样，是两个不同的集合(两棵不同的树)
  49.     if (root1 != root2) {
  50.       // 根据树的层数合并集合
  51.       // 
  52.       if (this.rank[root1] < this.rank[root2]) {
  53.         // 这个判断如果 root2 所在树的层数 大于 root1，就交换两个父节点，这样始终让 root1 为父节点
  54.         [root1, root2] = [root2, root1];
  55.       }
  56.       // 将层数多的集合合并到集合少的集合
  57.       this.parent[root2] = root1;
  58.       this.rank[root1] += this.rank[root2];
  59.       this.setCount--;
  60.     }
  61.   }
  63.   getCount() {
  64.     return this.setCount;
  65.   }
  67.   connected(index1, index2) {
  68.     let root1 = this.findSet(index1);
  69.     let root2 = this.findSet(index2);
  70.     return root1 == root2;
  71.   }
  72. }

广度优先搜索

对于每个城市，如果该城市尚未被访问过，则从该城市开始广度优先搜索，直到同一个连通分量中的所有城市都被访问到，即可得到一个身份。

  1. /**
  2.  * @param {number[][]} isConnected
  3.  * @return {number}
  4.  */
  5. var findCircleNum = function (isConnected) {
  6.   // 城市数量
  7.   const provinces = isConnected.length;
  8.   // 定义一个 Set 集合存储访问过的城市
  9.   const visited = new Set();
  10.   // 省份总数 (连同分量)
  11.   let circles = 0;
  12.   // 队列 queue 存储未被访问过的城市
  13.   const queue = new Array();
  14.   for (let i = 0; i < provinces; i++) {
  15.     if (!visited.has(i)) {
  16.       // 将城市放入队列中
  17.       queue.push(i);
  18.       while(queue.length) {
  19.         // 元素出队列
  20.         const j = queue.shift();
  21.         // 从queue队列中出队的城市已经被访问过，将其放入已访问的集合中
  22.         visited.add(j);
  23.         for (let k = 0; k < provinces; k++) {
  24.           if (isConnected[j][k] === 1 && !visited.has(k)) {
  25.             queue.push(k);
  26.           }
  27.         }
  28.       }
  29.       circles++;
  30.     }
  31.   }
  33.   return circles
  34. }

深度优先搜索

在深度优先搜索算法中，遍历所有城市，对于每个城市，如果该城市尚未被访问过，则从该城市开始深度优先搜索，通过矩阵 isConnected 得到与该城市直接相连的城市有哪些，这些城市和该城市属于同一个连通分量，然后对这些城市继续深度优先搜索，直到同一个连通分量的所有城市都被访问到，即可得到一个省份。遍历完全部城市后，即可得到连通分量的总数，即省份的总数。

  1. /**
  2.  * @param {number[][]} isConnected
  3.  * @return {number}
  4.  */
  5. var findCircleNum = function (isConnected) {
  6.   // 城市数量
  7.   const provinces = isConnected.length;
  8.   // 定义一个 Set 集合存储已被访问过的城市
  9.   const visited = new Set();
  10.   // 省份总数(连通分量总数)
  11.   let circles = 0;
  12.   for (let i = 0; i < provinces; i++) {
  13.     if (!visited.has(i)) {
  14.       dfs(isConnected, visited, provinces, i);
  15.       circles++
  16.     }
  17.   }
  19.   return circles;
  20. }
  22. const dfs = (isConnected, visited, provinces, i) => {
  23.   for (let j = 0; j < provinces; j++) {
  24.     if (isConnected[i][j] == 1 && !visited.has(j)) {
  25.       visited.add(j);
  26.       dfs(isConnected, visited, provinces, j);
  27.     }
  28.   }
  29. }