题目

题目来源：力扣（LeetCode）

树是一个无向图，其中任何两个顶点只通过一条路径连接。 换句话说，一个任何没有简单环路的连通图都是一棵树。
给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的 高度 是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：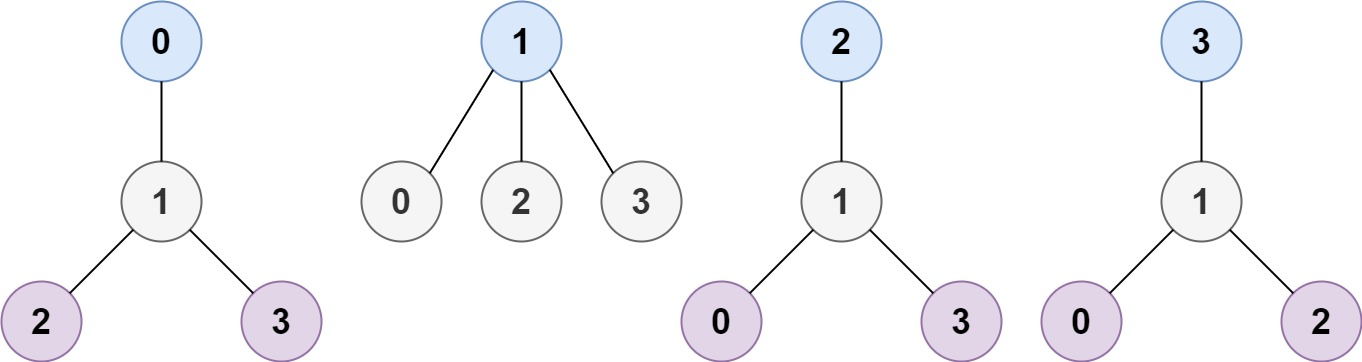
image.png
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：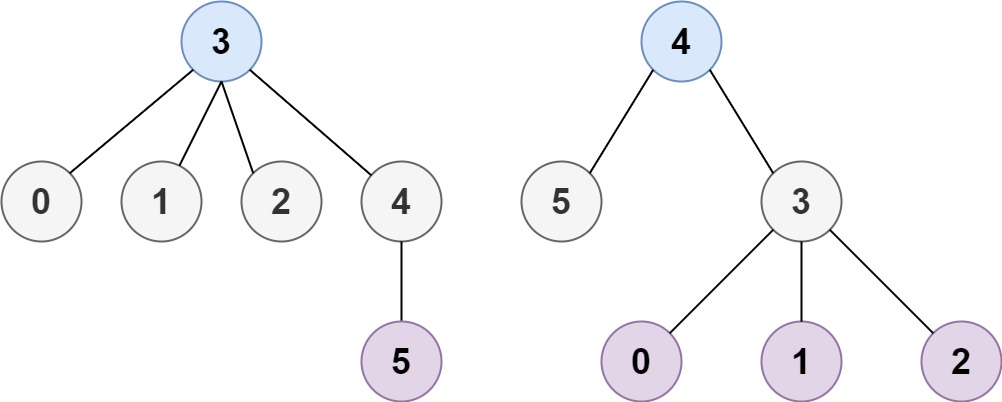
image.png
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

示例 3：

输入：n = 1, edges = []
输出：[0]

示例 4：

输入：n = 2, edges = [[0,1]]
输出：[0,1]

  1. /**
  2.  * @param {number} n
  3.  * @param {number[][]} edges
  4.  * @return {number[]}
  5.  */
  6. var findMinHeightTrees = function (n, edges) {
  7.   // check
  8.   if (n === 1 || edges.length === 0) return [0];
  9.   let root, len = edges.length, inDegs = new Array(n);
  10.   do {
  11.     // update length of edges
  12.     edges.length = len;
  13.     inDegs.fill(0);
  14.     for (let edge of edges) {
  15.       inDegs[edge[0]]++;
  16.       inDegs[edge[1]]++;
  17.     }
  18.     len = 0;
  19.     for (let edge of edges) {
  20.       // overwrite the value of edges if none of the edge's nodes is leaf
  21.       if (inDegs[edge[0]] > 1 && inDegs[edge[1]] > 1) edges[len++] = edge;
  22.       else if (inDegs[edge[0]] > 1) root = edge[0];
  23.       else if (inDegs[edge[1]] > 1) root = edge[1];
  24.     }
  25.   } while (len) // when len is 0, the edges hold the previous values
  26.   if (edges.length === 1) return edges[0]; // case 1
  27.   return [root]; // case 2
  28. };