题目

题目来源：力扣（LeetCode）

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格（即，(0, 0)）到 右下角 单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。
畅通路径的长度 是该路径途经的单元格总数。

示例 1：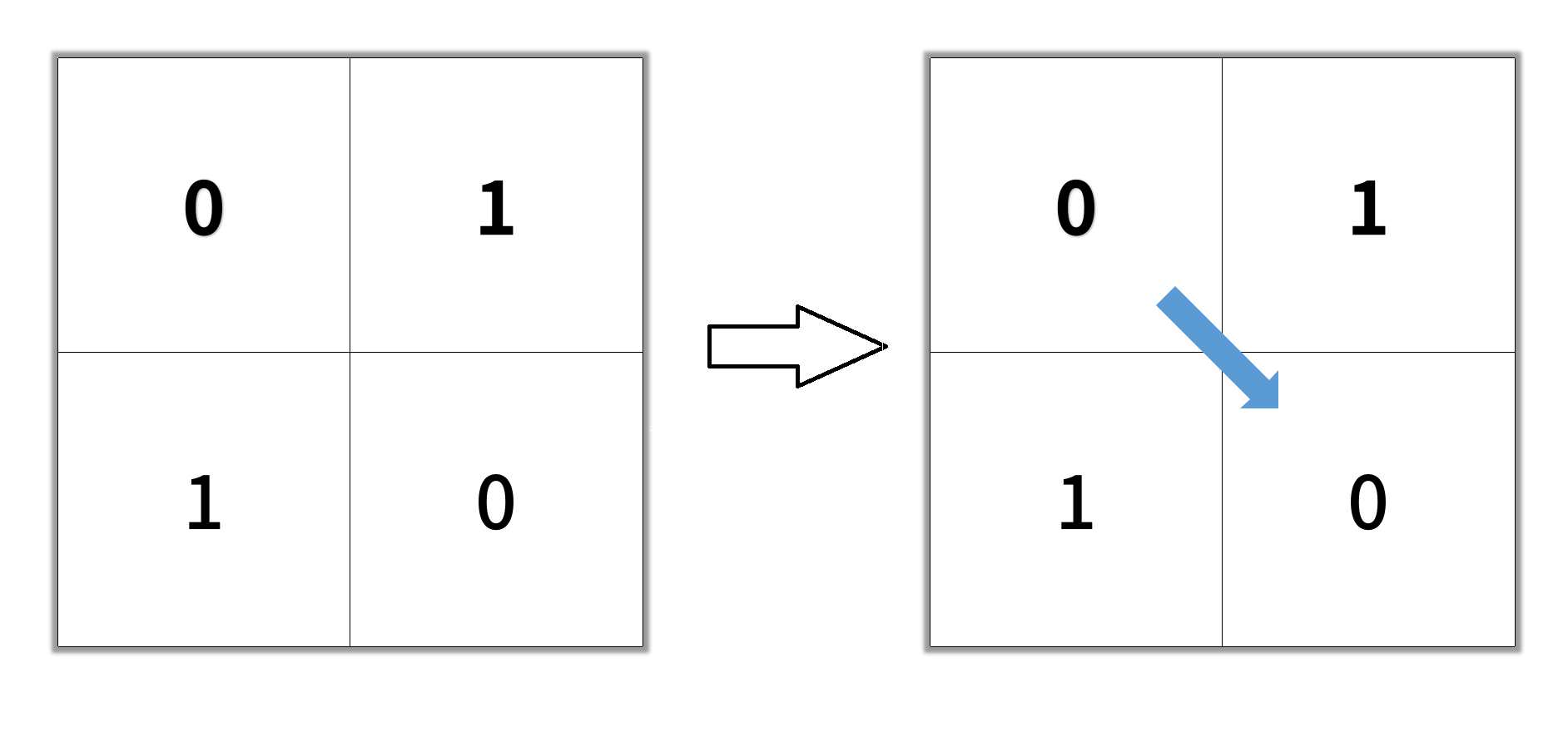
image.png
输入：grid = [[0,1],[1,0]]
输出：2

示例 2：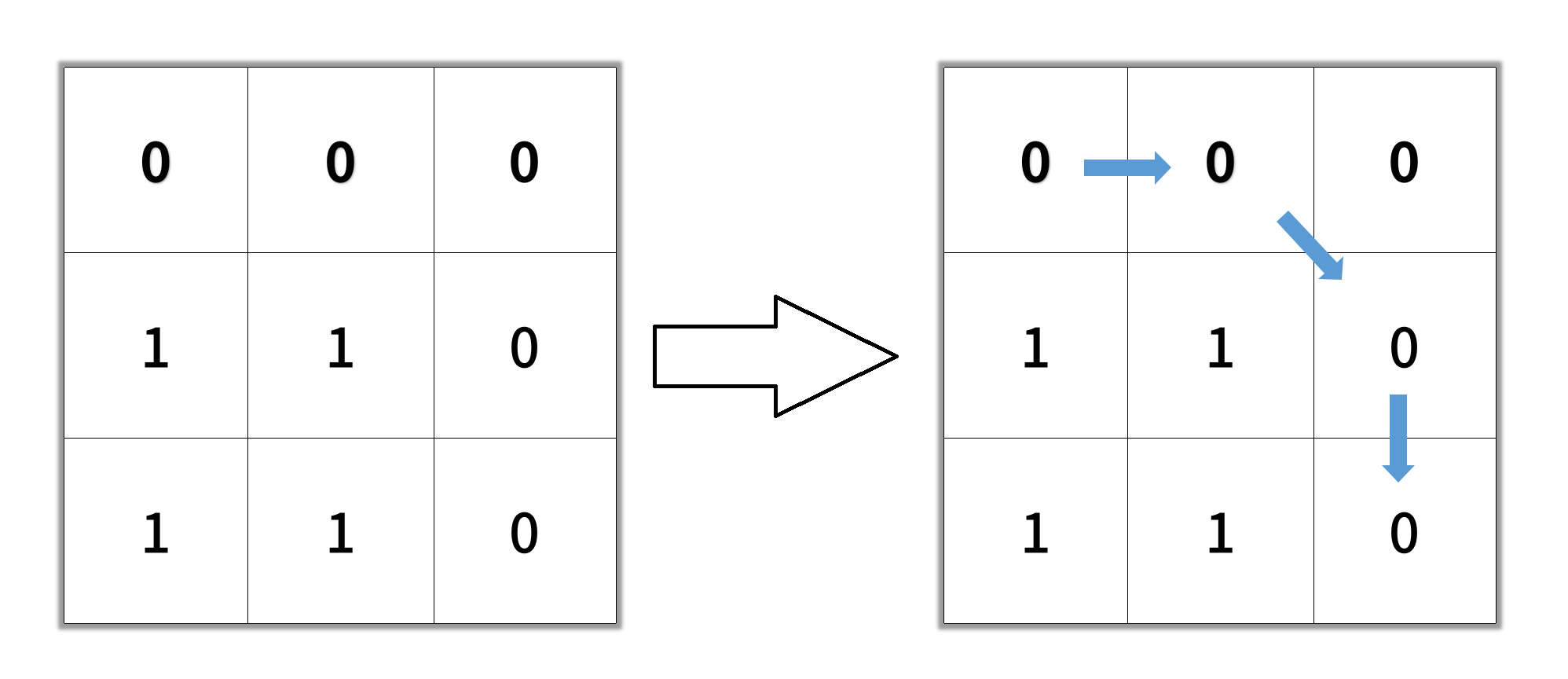
image.png
输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4

示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1

思路分析

  1. 从任意一个位置，都有8个方向可以走，每次走一步。但其中上、左、左上可以不用走，因为该题并 不存在遇到障碍物后需要往回走绕过的场景，只需要不断向右下方走即可。
  2. 使用BFS，每次循环都以当前一层节点为起点，向右下方扩散出下一层节点。每次走一层步数（即路径 长度）加1。
  3. 当遇到终点时，表示找到了最短路径，此时的层数就是路径长度
  1. // 下面我们来说bfs的具体队列是怎么实现的：
  2. // 1.将起点入队
  3. // 2.将起点（队首）可到达的节点全部入队，起点（队首）出队
  4. // 3.将队列的队首可到达的节点全部入队，队首出队
  6. // 依次下去，知道到达终点找到目标或者队列为空的时候，结束。
  8. var shortestPathBinaryMatrix = function (grid) {
  9.   // 缓存矩阵的终点位置
  10.   const m = grid.length - 1;
  11.   const n = grid[0].length - 1;
  12.   // 当起点和终点为1时，必然无法到达终点
  13.   if (grid[0][0] === 1 || grid[m][n] === 1) {
  14.     return -1;
  15.   }
  16.   // 如果矩阵只有1个点，且为0，路径为1
  17.   if (m === 0 && n === 0 && grid[0][0] === 0) {
  18.     return 1;
  19.   }
  20.   let queue = [[0, 0]]; // 使用队列进行BFS搜索
  21.   let level = 1; // 缓存路径长度，起点的长度为1
  22.   // 可以向四周所有方向行走，缓存8个方向
  23.   const direction = [
  24.     [-1, 1], // 右上
  25.     [0, 1], // 右
  26.     [1, 1], // 右下
  27.     [1, 0], // 下
  28.     [1, -1], // 左下
  29.     [-1, 0], // 上
  30.     [0, -1], // 左
  31.     [-1, -1], // 左上
  32.   ];
  33.   // 如果队列中有值，则继续搜索
  34.   while (queue.length) {
  35.     // 缓存当前层的节点数量
  36.     let queueLength = queue.length;
  37.     // 每次只遍历当前一层的节点
  38.     while (--queueLength >= 0) {
  39.       // 出队一个坐标，计算它可以行走的下一步位置
  40.       const [x, y] = queue.shift();
  42.       for (let i = 0; i < direction.length; i++) {
  43.         // 下一步可以向四周行走，计算出相应新坐标
  44.         const newX = x + direction[i][0];
  45.         const newY = y + direction[i][1];
  46.         // 如果新坐标超出网格，或者被标记为1，表示无法行走，则跳过
  47.         if (
  48.           newX < 0 ||
  49.           newY < 0 ||
  50.           newX > m ||
  51.           newY > m ||
  52.           grid[newX][newY] === 1
  53.         ) {
  54.           continue;
  55.         }
  56.         // 如果新坐标是终点，表示找到路径，返回长度即可
  57.         if (newX === m && newY === n) {
  58.           return level + 1;
  59.         }
  60.         // 将走过的位置标记为1，避免重复行走
  61.         grid[newX][newY] = 1;
  62.         // 将下一步的坐标存入队列，用于下一层循环
  63.         queue.push([newX, newY]);
  64.       }
  65.     }
  66.     level++; // 每向前走一层，将步数加1
  67.   }
  68.   return -1;
  69. };