二叉树 - 剑指 Offer 33. 二叉搜索树的后序遍历序列 - 《数据结构与算法》

题目
思路分析

题目

题目来源：力扣（LeetCode）

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

 5<br />    / \<br />   2   6<br />  / \<br /> 1   3<br />示例 1：

输入: [1,6,3,2,5]
输出: false
示例 2：

输入: [1,3,2,6,5]
输出: true

思路分析

二叉搜索树具有以下性质：

若任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不为空，则右子树上所有子节点的值均大于它的根节点的值；
任意节点的左、右子树也分别为二叉搜索树；

我们简化一下上面的文字，二叉搜索树的性质为：左子树的值 < 根节点 < 右子树的值 ，二叉搜索树的后续遍历是：左子树 -> 右子树 -> 根节点 。

方法一：递归分治

根据二叉搜索树的性质，可以通过递归，判断所有子树的后序遍历是否满足二叉搜索树的性质，若所有子树都满足，则该数组是二叉搜索树的后序遍历结果。

划分左右子树

将数组的第一个索引记为 left，最后一个索引记为 right，则二叉搜索树的后序遍历结果可表示为 [left, right] 的区间元素。

我们知道后续遍历的最后一个数字一定是根节点，所以数组中最后一个数字就是根节点。我们从前往后遍历 [left, right] 区间元素，找到 第一个大于根节点的节点，其索引记为 m，可根据 m 划分出左子树区间 [m, m - 1]，右子树区间 [m, right - 1]，根节点为索引 right 。

比如下面这棵二叉树，它的后序遍历结果为：[5, 9, 7, 13, 15, 11]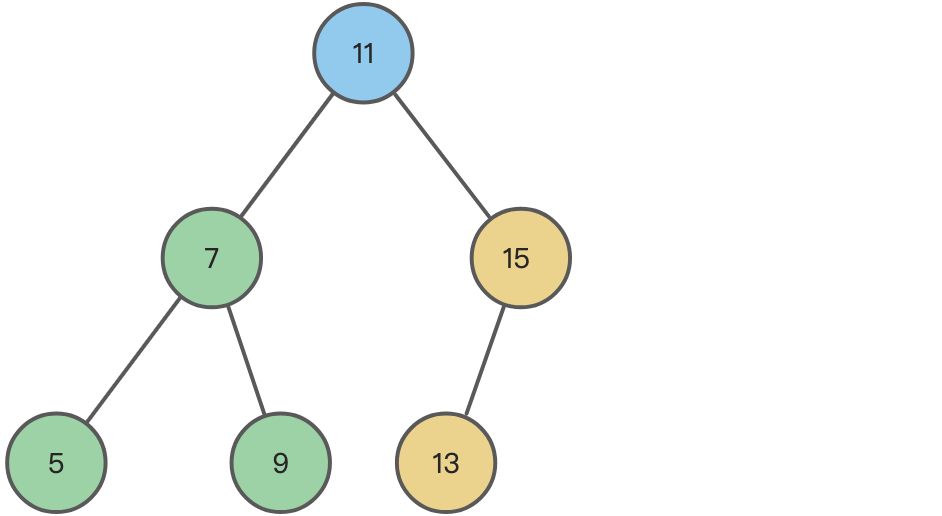
剑指 Offer 33. 二叉搜索树的后序遍历序列 - 图1
数组中最后一个数字 11 就是根节点，我们从前完后遍历数组，找到第一个比 11 大的数字 13，那么 13 后面的 [13, 15] （除了11，包括13）都是 11 的右子树，13 前面的 [5, 9, 7] 都是 13 的左子树。

判断是否为二叉搜索树

左子树区间：[left, m - 1] 区间内的所有节点都应小于根节点nums[right] ，而「划分左右子树」步骤已经保证左子树区间的正确性，因此只需要判断右子树区间即可。
右子树区间：[m, right - 1] 区间内的所有节点都应大于根节点nums[right] 。

返回值：所有子树都为二叉搜索树才可返回true，否则返回 false

代码

/**
 * @param {number[]} postorder
 * @return {boolean}
 */
 var verifyPostorder = function(postorder) {
  return inOrder(postorder, 0, postorder.length - 1)
};
var inOrder = function(postorder, left, right) {
  // 如果 left >= right，说明此子树节点数量 <= 1 ，无需判别正确性，因此直接返回 true
  if (left >=right) return true;
  // 数组最后一个值 postorder[right] 是根节点，这里从左往右遍历数组，找出第一个比根节点大的值
  // 这个值后面的都是根节点的右子节点(包含当前值，不包含最后一个值, 即 [mid, right - 1])
  // 这个值前面的都是根节点的左子节点(不包含当前值，即 [left, mid - 1])
  let mid = left;
  const root = postorder[right];
  // 找出第一个比根节点大的值
  while(postorder[mid] < root) {
    mid++
  }
  // mid 前面的值都是比根节点小的，我们还需要判断 mid 后面的值是否都比根节点root 大
  // 如果 mid 后面有比根节点小的值，说明右子树不是二叉搜索树，那么返回false
  let temp = mid;
  while(temp < right) {
    // 在 [mid, right - 1] 区间若有小于根节点的值，返回 false
    if (postorder[temp++] < root) return false;
  }
  // 对左右子树进行递归判断是否为二叉搜索树
  return inOrder(postorder, left, mid - 1) && inOrder(postorder, mid, right - 1)
}

方法二：单调递增栈

二叉搜索树的后序遍历顺序为：左子树 -> 右子树 -> 根节点
那么后序遍历的倒序为：根节点 -> 右子树 -> 左子树

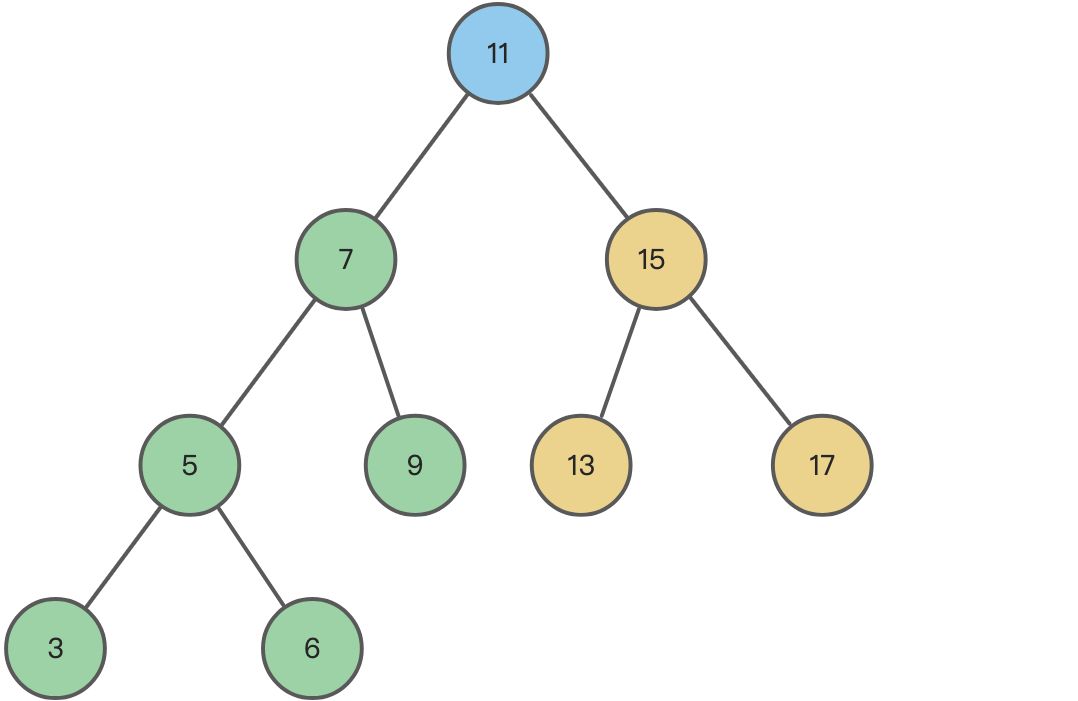
剑指 Offer 33. 二叉搜索树的后序遍历序列 - 图2
如上图中的二叉搜索树，它的后序遍历结果是： [3, 6, 5, 9, 7, 13, 17, 15, 11]
它的后序遍历结果的倒序为：[11, 15, 17, 13, 7, 9, 5, 6, 3] (下文称该数组为 reverseArr)

规律一
我们仔细观察reverseArr数组，我们会发现一个规律：挨着的两个数，如果前面的数小于后面的数，即
**reverseArr[i] < reverseArr[i + 1]**，那么 reverseArr[i+ 1] 一定是 arr[i] 的右子节点，可根据后序遍历的倒序顺序 根节点 -> 右子树 -> 左子树 得出。

在 reverseArr 数组中，11 和 15 是挨着的，并且 11 < 15，所以 15 是 11 的右子节点。同理 13 和 17、7 和 9、5 和 6，它们都是挨着的，并且都是前面的数小于后面的数，根据后序遍历的倒序顺序，我们可以得出后面的数都是前面的右子节点

规律二
我们继续观察reverseArr数组，同样是挨着的两个数，如果前面的数大于后面的数，即 **reverseArr[i] > reverseArr[i + 1]** ，那么 reverseArr[i + 1] 一定是 reverseArr[0], … reverseArr[i] 中某给节点的左子节点，并且这个值是大于 reverseArr[i + 1] 中最小的。

在 reverseArr 数组中，17 和 13 是挨着的，并且 17 > 13，那么 13 肯定是它前面某一个节点的左子节点，并且这个值是大于 13 中最小的，在 13 前面的两个数 17 和 15 都是大于它的，但 15 最小，所以 15 就是 13 的左子节点。同理我们可以观察到 13 和 7 也是挨着的，7 前面的数(它们是：11, 15, 17, 13)大于 7 的最小的数是 11，所以 7 就是 11 的左子节点。9 和 5，6 和 3 都是挨着的，并且都是前面的数大于后面的数，因此同样遵守这个规律。

根据上面的两个规律，我们借助一个单调递增栈存储值递增的节点。

遍历reverseArr数组的所有元素：

如果栈为空，就把当前元素入栈
如果栈不为空，判断当前元素是否大于栈顶元素：
1. 如果当前元素大于栈顶元素，根据规律一，那么当前元素是栈顶元素的右子节点，把当前元素入栈，如果继续遍历的元素一直大于栈顶元素，元素就一直入栈
2. 如果当前元素小于栈顶元素，根据规律二，那么当前元素是某个节点的左子节点，我们的目的是要找到这个左子节点的父节点，就让栈顶元素出栈，直到栈为空或者栈顶元素小于当前元素为止，其中最后一个出栈的就是当前元素的父节点

代码

/**
 * @param {number[]} postorder
 * @return {boolean}
 */
 var verifyPostorder = function(postorder) {
  const stack = []; // 单调递增栈存储值递增的节点
  let parent = Infinity; // 将父节点值初始化为正无穷大
  // 倒序遍历二叉搜索树的后序遍历结果
  for (let i = postorder.length - 1; i >= 0; i--) {
    // 当前遍历的元素
    const cur = postorder[i];
    // 如果栈不为空并且当前节点小于栈顶节点，说明当前节点是前面某个节点的左子节点，我们要找到它的父节点
    // 因此栈顶元素出栈，直到栈为空或者栈顶元素小于当前元素为止
    // 最后一个出栈的元素就是当前节点的父节点
    while(stack.length && stack[stack.length - 1] > cur) parent = stack.pop();
    // 只要遇到了某一个左子节点，才会执行上面的代码，才会更新parent的值，
    // 否则parent就是一个非常大的值，也就是说如果一直没有遇到左子节点，那么右子节点可以非常大
    // parent并不一定都是父节点的值，相对于遇到了左子节点的时候他是左子节点的父节点。
    // 如果是右子节点，parent就是他的某一个祖先节点，并且这个右子节点是这个祖先节点的一个左子树的一部分，所以不能超过他
    if (cur > parent) return false;
    // 若栈为空，当前元素入栈
    // 当前元素大于栈顶元素，说明当前元素是栈顶元素的右子节点，那么当前元素入栈
    stack.push(cur)
  }
  return true;
};