数据结构 - 数据结构与算法学习之二叉堆 - 《数据结构与算法》

二叉堆数据结构
- 最大堆
- 最小堆
实现最小堆
实现最大堆
- 创建最大堆类
- reverseCompare

二叉堆数据结构

二叉堆是一种特殊的二叉树，它具有以下两个特性：

结构特性：它是一棵完全二叉树，表示树的每一层都有左侧和右侧子节点(除了最后一层的叶节点)，并且最后一层的叶节点尽可能都是左侧子节点。
堆特性：二叉堆不是最小堆就是最大堆。最小堆允许你快速导出树的最小值，最大堆允许你快速导出数的最大值。

最大堆

父节点的键值总是大于或等于任何一个子节点的键值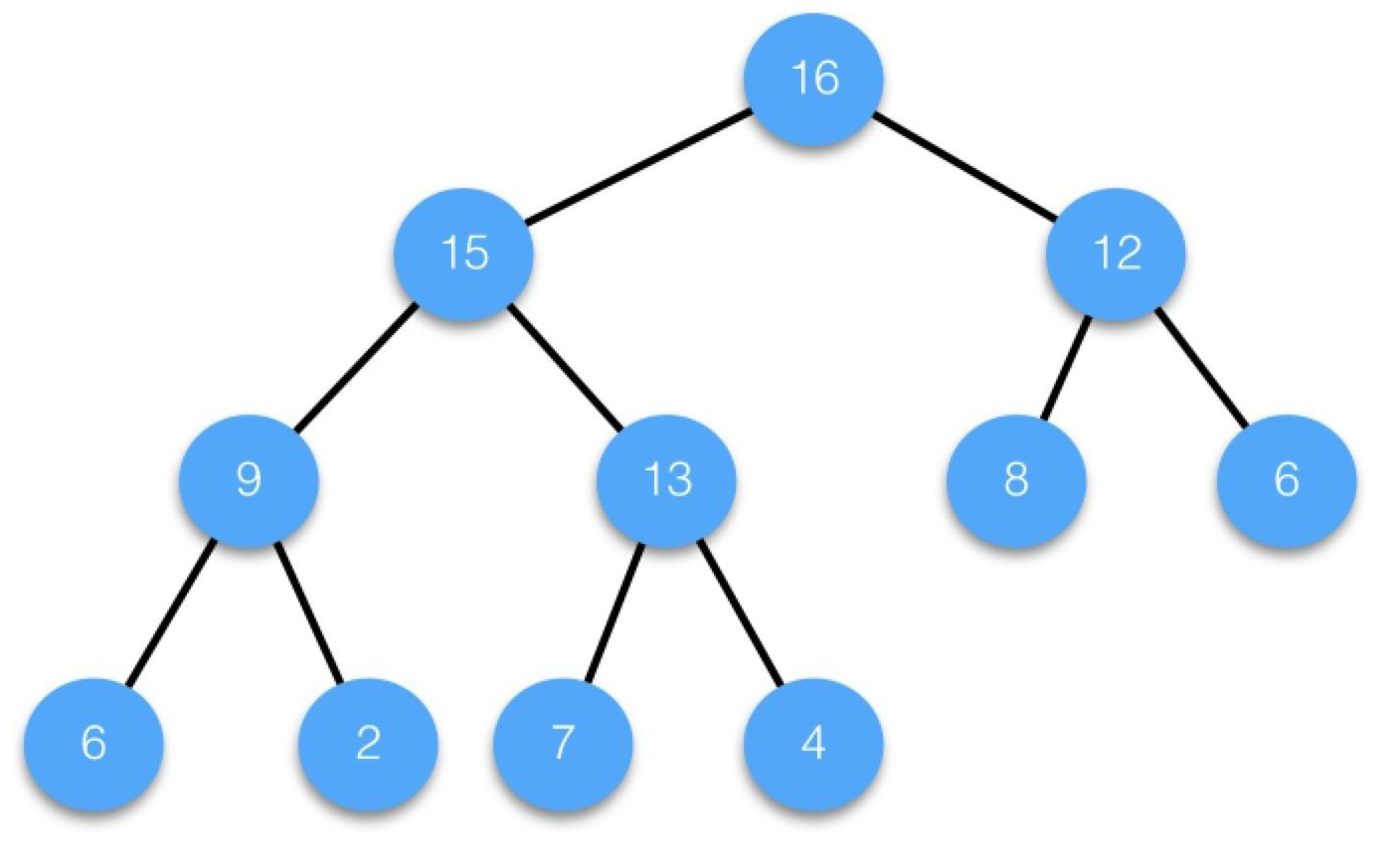最大堆.png

最小堆

父节点的键值总是小于或等于任何一个子节点的键值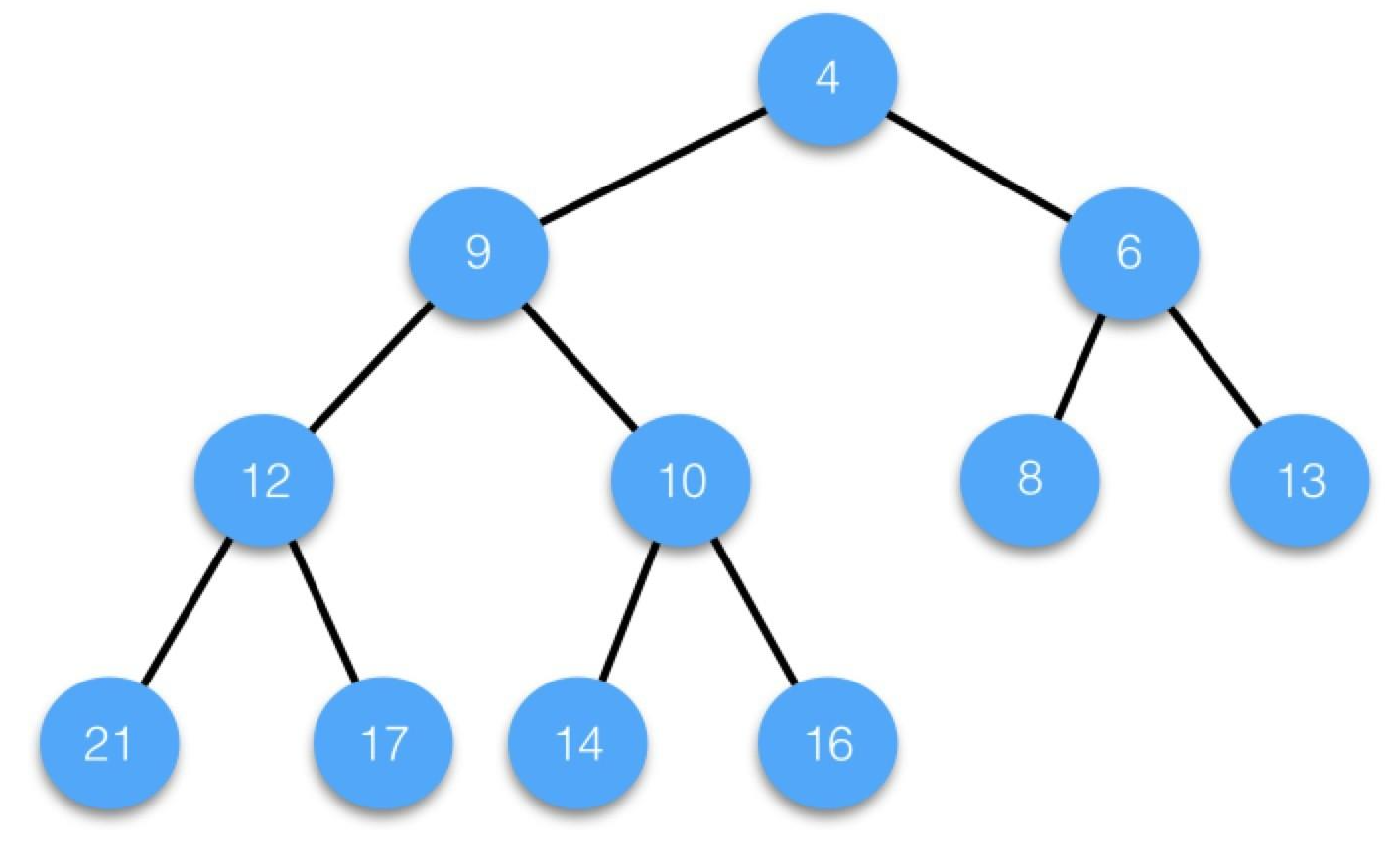最小堆.png

实现最小堆

创建最小堆类

在 constructor 构造函数中，定义 compareFn 函数来比较存储在数据结构中的值，使用数组来存储数据。

class MinHeap {
  constructor(compareFn = defaultCompare) {
    this.compareFn = compareFn;
    this.heap = [];
  }
}

声明 Compare 常量

export const Compare = {
  LESS_THAN: -1,
  BIGGER_THAN: 1,
  EQUALS: 0
};

创建 defaultCompare 函数

export function defaultCompare(a, b) {
  if (a === b) {
    return Compare.EQUALS;
  }
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}

在本文中，我们使用数组来存储二叉堆的节点，因此我们可以通过 index 来获取二叉堆的节点。对于给定位置 index 的节点：

它的左侧子节点的位置是 2 * index + 1
它的右侧子节点的位置是 2 * index + 2
它的父节点位置（index - 1）/ 2

根据以上规则，我们来实现获取节点的方法。

getLeftIndex - 获取左侧子节点

getLeftIndex(index) {
  return (2 * index) + 1;
}

getRightIndex - 获取右侧子节点

getRightIndex(index) {
  return (2 * index) + 2;
}

getParentIndex - 获取父节点

getParentIndex(index) {
  if (index === 0) {
    return undefined;
  }
  return Math.floor((index - 1) / 2);
}

insert - 向堆中插入值

insert(value) {
    if (value != null) {
    const index = this.heap.length;
    // 将值插入到堆的底部叶节点(即数组的最后一个位置)
      this.heap.push(value);
    // 将插入的值和它的父节点进行交换，直到父节点小于这个插入的值
    this.siftUp(index);
    // 插入成功，返回 true
    return true;
  }
  // 插入失败，返回 false
  return false;
}

将值插入到堆的底部叶节点 (即数组的最后一个位置)，然后执行 siftUp 方法，将插入的值和它的父节点进行交换，直到父节点小于这个插入的值。

siftUp - 上移操作

siftUp(index) {
  // 获取父节点的位置
    let parent = this.getParentIndex(index);
  while (
      index > 0 &&
      this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
    ) {
    // 在最小堆中，如果插入的值小于它的父节点(或者在最大堆中比父节点大)，将这个元素和父节点交换
      swap(this.heap, parent, index);
    // 交换节点位置
    index = parent;
    parent = this.getParentIndex(index);
  }
}

swap 交换函数

function swap(array, a, b) {
    const temp = array[a];
  array[a] = array[b];
  array[b] = temp;
}

在 swap 函数中，定义了一个 temp 变量来缓存要交换的第一个元素，然后，将第二个元素赋值到第一个元素的位置 array[a] = array[b]; ，最后，将缓存起来的第一个元素的值覆盖到第二个元素的值 array[b] = temp; 。

也可以使用 ES6 的数组结构语法实现 swap 函数：

const swap = (array, a, b) => [array[a], array[b]] = [array[b], array[a]];

size - 获取堆中数据的长度

size() {
    return this.heap.length;
}

isEmpty - 判断堆是否为空

isEmpty() {
  return this.size() <= 0;
}

clear - 清空堆

this.heap = [];

findMinimum - 查找堆中最小值

findMinimum() {
    return this.isEmpty() ? undefined : this.head[0];
}

在最小堆中，最小值总是位于数组的第一个位置(堆的根节点)。在最大堆中，数组的第一个元素就是最大的值(堆的根节点)，因此可以使用相同的代码获取最大堆的最大值。

extract - 导出堆中的最小值或最大值

extract() {
  // 堆为空，也就是没有值可以导出，返回 undefined
    if (this.isEmpty()) {
      return undefined;
  }
  // 堆中只有一个值，直接移除并返回这个值
  if (this.size() === 1) {
      return this.heap.shift();
  }
  // 将需要移除的值缓存起来
  const removedValue = this.heap.shift();
  // 将堆的最后一个元素移动至根部
  this.heap[0] = this.heap.pop();
  // 从根元素开始交换元素，直至堆的结构正常
  this.siftDown(0);
  return removedValue;
}

移除最小值(最小堆) 或最大值(最大堆)，也就是要移除数组中的第一个元素 (堆的根节点)。在移除后，我们需要将堆的最后一个元素移动至根部并执行 siftDown 函数，将堆中的元素进行交换直至堆的结构正常。

siftDown - 下移操作

// 接收移除元素的位置作为参数
siftDown(index) {
    let element = index;
  // 获取左侧子节点的位置
  const left = this.getLeftIndex(index);
  // 获取右侧子节点的位置
  const right = this.getRightIndex(index);
  // 获取堆的长度
  const size = this.size();
  // 如果元素 this.heap[element] 比它的左侧子节点要小，交换元素和它的左侧子节点
  if (
    left < size &&
    this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN
  ) {
    element = left;
  }
  // 如果元素小于 this.heap[element] 小于它的右侧子节点，交换元素和它的右侧子节点
  if (
    right < size &&
    this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
  ) {
    element = right;
  }
  // 在找到最小子节点的位置后，校验它的值是否和 element 相同，不同，则进行交换
  if (index !== element) {
    swap(this.heap, index, element);
    this.siftDown(element);
  }
}

heapify

heapify(array) {
  if (array) {
    this.heap = array;
  }
  const maxIndex = Math.floor(this.size() / 2) - 1;
  for (let i = 0; i <= maxIndex; i++) {
    this.siftDown(i);
  }
  return this.heap;
}

getAsArray

getAsArray() {
    return this.heap;
}

完整代码

export class MinHeap {
  constructor(compareFn = defaultCompare) {
    this.compareFn = compareFn;
    this.heap = [];
  }
  // 获取左侧子节点位置
  getLeftIndex(index) {
    return (2 * index) + 1;
  }
  // 获取右侧子节点位置
  getRightIndex(index) {
    return (2 * index) + 2;
  }
  // 获取父节点位置
  getParentIndex(index) {
    if (index === 0) {
      return undefined;
    }
    return Math.floor((index - 1) / 2);
  }
  // 堆的大小
  size() {
    return this.heap.length;
  }
  // 是否为空堆
  isEmpty() {
    return this.size() <= 0;
  }
  // 清空堆
  clear() {
    this.heap = [];
  }
  // 查找堆的最小值、最大值
  findMinimum() {
    return this.isEmpty() ? undefined : this.heap[0];
  }
  // 向堆中插入值
  insert(value) {
    if (value != null) {
      const index = this.heap.length;
      this.heap.push(value);
      this.siftUp(index);
      return true;
    }
    return false;
  }
  // 下移操作
  siftDown(index) {
    let element = index;
    const left = this.getLeftIndex(index);
    const right = this.getRightIndex(index);
    const size = this.size();
    if (
      left < size &&
      this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN
    ) {
      element = left;
    }
    if (
      right < size &&
      this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
    ) {
      element = right;
    }
    if (index !== element) {
      swap(this.heap, index, element);
      this.siftDown(element);
    }
  }
  // 节点上移操作
  siftUp(index) {
    let parent = this.getParentIndex(index);
    while (
      index > 0 &&
      this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
    ) {
      swap(this.heap, parent, index);
      index = parent;
      parent = this.getParentIndex(index);
    }
  }
  // 导出堆中的最小值或最大值
  extract() {
    if (this.isEmpty()) {
      return undefined;
    }
    if (this.size() === 1) {
      return this.heap.shift();
    }
    const removedValue = this.heap[0];
    this.heap[0] = this.heap.pop();
    this.siftDown(0);
    return removedValue;
  }
  heapify(array) {
    if (array) {
      this.heap = array;
    }
    const maxIndex = Math.floor(this.size() / 2) - 1;
    for (let i = 0; i <= maxIndex; i++) {
      this.siftDown(i);
    }
    return this.heap;
  }
  getAsArray() {
    return this.heap;
  }
}

实现最大堆

最大堆的实现和最小堆的实现是一模一样的，不同之处在于我们要把所有 > (大于) 的比较换成 < (小于) 的比较。

创建最大堆类

class MaxHeap extends MinHeap {
    constructor (compareFn = defaultCompare) {
      super(compareFn);
    this.compareFn = reverseCompare(compareFn);
  }
}

我们通过继承 MinHeap 类来实现最大堆，并定义了一个 reverseCompare 函数进行反向比较，也就是不再对 a 和 b 进行比较，而是将 b 和 a 进行比较。

reverseCompare

function reverseCompare(compareFn) {
    return (a, b) => compareFn(b, a);
}