题目

题目来源：力扣（LeetCode）

设计一个算法，找出二叉搜索树中指定节点的“下一个”节点（也即中序后继）。

如果指定节点没有对应的“下一个”节点，则返回null。

示例 1:

输入: root = [2,1,3], p = 1

2
/ \
1 3

输出: 2

示例 2:

输入: root = [5,3,6,2,4,null,null,1], p = 6

  1.   5<br />     / \<br />    3   6<br />   / \<br />  2   4<br /> /   <br />1

输出: null

思路分析

二叉搜索树的中序遍历结果是一个递增的有序序列，找出 p 的后继节点，就是在中序遍历结果的有序序列中找到比 p 大的下一个节点。

递归解法

  • 如果节点p 的值大于等于当前节点node 的值，说明 p 的后继节点在 node节点的右子树中，那么就递归到右子树中查找
  • 如果节点p 的值小于当前节点node 的值，说明节点p 在节点node 的左子树中，那么 p 的后继节点有两种可能，要么也在左子树中，要么就是节点node
    • 如果在左子树中找到了后继节点，那就直接返回答案
    • 如果在左子树中没有找到后继节点，那说明节点p 的右孩子为空，那么节点node 就是节点p 的后继节点
  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val) {
  4.  *     this.val = val;
  5.  *     this.left = this.right = null;
  6.  * }
  7.  */
  8. /**
  9.  * @param {TreeNode} root
  10.  * @param {TreeNode} p
  11.  * @return {TreeNode}
  12.  */
  13.   var inorderSuccessor = function(root, p) {
  14.   if (root == null || p == null) return null;
  15.   // 如果节点p 的值大于等于当前节点node 的值，说明 p 的后继节点在 node节点的右子树中，那么就递归到右子树中查找
  16.   if (p.val >= root.val) {
  17.     return inorderSuccessor(root.right, p)
  18.   } else {
  19.     // 如果节点p 的值小于当前节点node 的值，说明节点p 在节点node 的左子树中，那么 p 的后继节点有两种可能，要么也在左子树中，要么就是节点node
  20.     // 如果在左子树中找到了后继节点，那就直接返回答案
  21.     // 如果在左子树中没有找到后继节点，那说明节点p 的右孩子为空，那么节点node 就是节点p 的后继节点
  22.     const left = inorderSuccessor(root.left, p);
  23.     return left ? left : root
  24.   }
  25. };

非递归

  • 如果节点p 有右子节点，那么它的后继节点就是右子树中最左边的子节点

  • 如果节点p 没有右子节点，那么它的右子节点就是，沿着节点p 往上到节点root 的路径中，第一个左孩子在路径上的节点。因为这个节点的左子树中 p 是最右边的结点，是最大的，所以它就是 p 的后继结点。因为是二叉搜索树，我们就可以从根节点开始往 p 走，根据节点值的大小决定走的方向。

对于第二种情况，解析如下：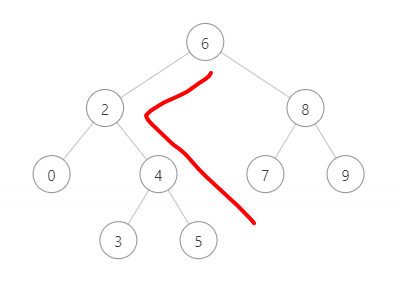
image.png
我们这里用5举例，首先我们根据二叉搜索树的性质遍历找到节点5的位置，并检查其不存在右子树。
根据中序遍历，我们知道5的后继节点应该是6。我们观察一下从6到5这个路径（图中红线），可以得到是从6左转一次，然后一直往右边走直到找到5的。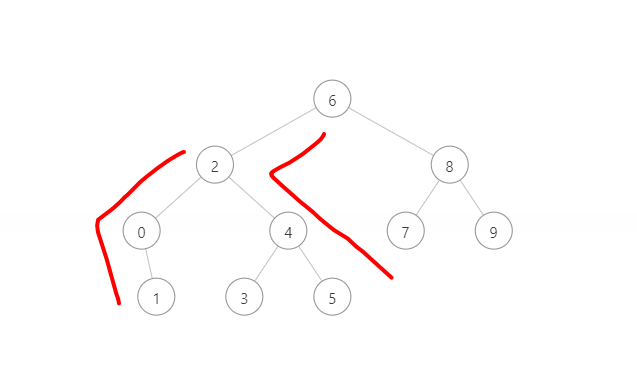
image.png
我们再看一下2 -> 0 -> 1，这两个路径，也是从2左转一次，然后一直往右走直到找到1的。那我们就得到此方案：在左转之前，将当前结点记录一下。比如在寻找5，在节点6时判断，是要左转的，那么用pre记录一下6这个节点。假如5没有右子树，那么就可以返回pre了，假如路径中发生了新的左转动作，那么pre也需要更新。

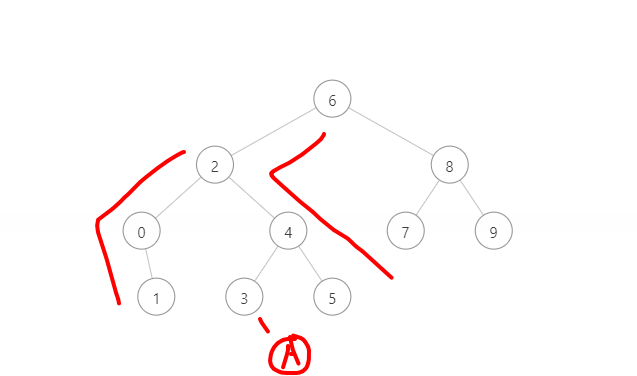
image.png
例如我要找A，他的后继节点是4
这里在6左转了一次，pre=6，但在4这里比较，发现需要左转，那么更新pre=4。
假如是在9这里，这里一次左转都没有，因为pre初始值是null，这里直接返回null即可。

  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val) {
  4.  *     this.val = val;
  5.  *     this.left = this.right = null;
  6.  * }
  7.  */
  8. /**
  9.  * @param {TreeNode} root
  10.  * @param {TreeNode} p
  11.  * @return {TreeNode}
  12.  */
  13. var inorderSuccessor = function (root, p) {
  15.   let pre = null;
  16.   while (root.val != p.val) {
  17.     //右边
  18.     if (p.val > root.val) {
  19.       root = root.right;
  20.     }
  21.     //左边
  22.     else {
  23.       pre = root;
  24.       root = root.left;
  25.     }
  26.   }
  27.   //假如没有右子树
  28.   if (root.right == null) {
  29.     return pre;
  30.   }
  31.   else {
  32.     root = root.right;
  33.     while (root.left != null) {
  34.       root = root.left;
  35.     }
  36.     return root;
  37.   }
  39. }

参考 https://leetcode-cn.com/problems/successor-lcci/solution/100liang-chong-qing-kuang-zhi-xu-yao-yi-ghpai/ https://leetcode-cn.com/problems/successor-lcci/solution/zhong-xu-bian-li-de-xia-yi-ge-yuan-su-5da-jie-fa-h/