题目

题目来源：力扣（LeetCode）

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：
image.png
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

解法一：单调栈

可以用单调栈计算能接的雨水总量。

维护一个单调栈，单调栈存储的是下标，满足从栈底到栈顶的下标对应的数组 height 中的元素递减。

从左到右遍历数组，遍历到下标 i 时，如果栈内至少有两个元素，记栈顶元素为 top，top 的下面一个元素是 left，则一定有 height[left] ≥ height[top]。

如果当前遍历的元素大于栈顶元素：height[i] > height[top]，则得到一个可以接雨水的区域，该区域的宽度是 i - left -1，高度是 min(height[left], height[i]) - height[top]，根据宽度和高度即可计算得到该区域能接的雨水量。

为了得到 left，需要将 top 出栈。在对 top 计算能接的雨水量之后，left 变成新的 top，重复上述操作，直到栈变为空，或者栈顶下标对应的 height 中的元素大于或等于 height[i]。

在对下标 i 处计算能接的雨水量之后，将 i 入栈，继续遍历后面的下标，计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。

  1. /**
  2.  * @param {number[]} height
  3.  * @return {number}
  4.  */
  5. var trap = function (height) {
  6.   let ans = 0;
  7.   // 单调递减栈，维护的是下标，栈底到栈顶的下标对应的数组 height 中的元素递减
  8.   const stack = [];
  9.   // 数组的长度
  10.   const n = height.length;
  11.   // 从左到有遍历数组，遍历到下标 i 时，如果栈内至少有两个元素，记栈顶元素为 top，top 下面的一个元素是 left，则一定有 height[left] ≥ height[top]
  12.   for (let i = 0; i < n; ++i) {
  13.     // 如果当前遍历的元素 height[i] > 栈顶元素 height[stack[stack.length - 1]]，栈顶元素出栈
  14.     // 说明得到一个可以接水的区域，该区域的宽度是 i−left−1，高度是 min(height[left],height[i])−height[top]
  15.     // 其实就是 栈顶和栈顶的下一个元素以及要入栈的三个元素来接水
  16.     while (stack.length && height[i] > height[stack[stack.length - 1]]) {
  17.       // 栈顶元素出栈
  18.       const top = stack.pop();
  19.       // 直到栈变为空，或者栈顶下标对应的height 中的元素大于或等于 height[i]，退出 while 循环
  20.       if (!stack.length) {
  21.         break;
  22.       }
  24.       const left = stack[stack.length - 1];
  25.       // 可接水区域的宽度，凹槽右边的下标 - 凹槽左边的下标 - 1（因为只求中间宽度)
  26.       const currWidth = i - left - 1;
  27.       // 可接水区域的高度，min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
  28.       const currHeight = Math.min(height[left], height[i]) - height[top];
  29.       // 累加雨水的体积
  30.       ans += currWidth * currHeight;
  31.     }
  32.     // 在对下标 i 处计算能接的雨水量之后，将 i 入栈，继续遍历后面的下标，计算能接的雨水量
  33.     stack.push(i);
  34.   }
  35.   return ans;
  36. };

解法二：数学解法

前置知识：维恩图

维恩图 用于展示在不同的事物群组（集合）之间的数学或逻辑联系，尤其适合用来表示集合（或）类之间的“大致关系”，它也常常被用来帮助推导（或理解推导过程）关于集合运算（或类运算）的一些规律。

从左往右遍历，无论是雨水还是柱子，都将它们的面积计算在有效面积内，并且每次累加的值都会随着遍历到的最高的柱子逐步上升。如下图，浅绿色部分的面积加上深绿色部分的面积(即柱子的面积) 为有效面积，将其计为 S1，如下图：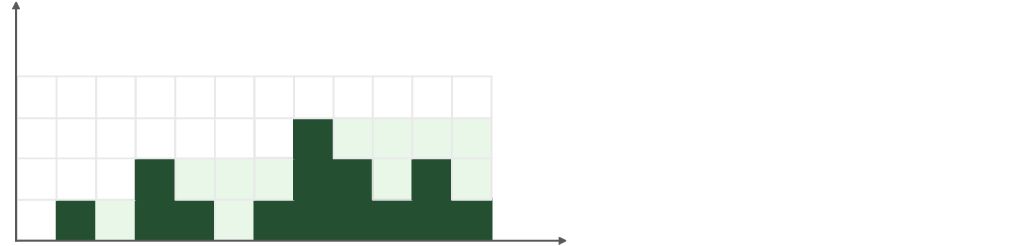
接雨水 - 图2
从左往右遍历，累加得 S1，将每步遍历到的面积记为 maxLeft，每步 S1 += maxLeft 且 maxLeft 逐步增大

同样地，从右往左遍历，将雨水和柱子的面积计算在有效面积内，并且每次累加的值也会随着遍历到的最高的柱子逐步上升。如下图，浅粉色部分的面积加上深红色的面积(柱子的面积) 为有效面积，将其记为 S2，如下图：
接雨水 - 图3
从右往左遍历，累加得 S2，将每步遍历到的面积记为 maxRight，每步 S2 += maxRight 且 maxRight 逐步增大

将 S1 和 S2 相加，刚好是一个矩形。如下图：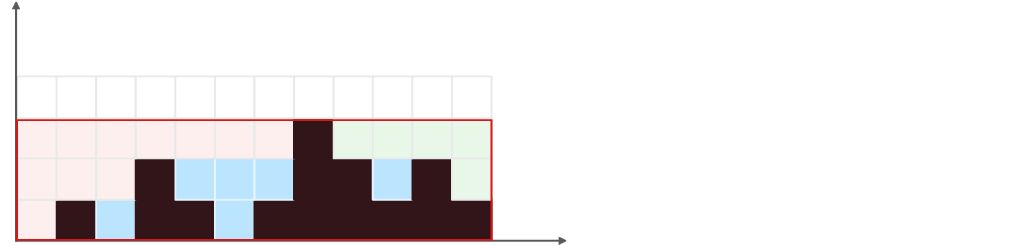
接雨水 - 图4
在上图中，将浅粉色的面积记为 Spink，浅绿色的面积记为Sgreen。由于 S1 中包含了积水面积和柱子面积，S2 中同样包含了积水面积和柱子面积，S1 和 S2 相加，则必然会有：重复面积 = 2 (积水面积 + 柱子面积)。因此：
S1 加 S2 的面积：S1 + S2 = Spink + Sgreen + 重复面积
即：S1 + S2 = Spink + Sgreen + 2 (积水面积 + 柱子面积)

矩形的面积：矩形面积 = Spink + Sgreen + 积水面积 + 柱子面积

由此可得：S1 + S2 = 矩形面积 + 柱子面积 + 积水面积

最终可得：积水面积 = S1 + S2 - 矩形面积 - 柱子面积

  1. /**
  2.  * @param {number[]} height
  3.  * @return {number}
  4.  */
  5. var trap = function (height) {
  6.   // 韦恩图解法
  7.   const len = height.length;
  8.   let s1 = 0;
  9.   let s2 = 0;
  10.   // 柱子面积
  11.   let sum = 0;
  12.   // 从左往右遍历，当前柱子的最大面积
  13.   let maxLeft = 0
  14.    // 从右往左遍历，当前柱子的最大面积
  15.   let maxRight = 0;
  16.   for (let i = 0; i < len; i++) {
  17.     // if (height[i] > maxLeft) {
  18.     //   maxLeft = height[i];
  19.     // }
  20.     // if (height[len - i - 1] > maxRight) {
  21.     //   maxRight = height[len - i - 1];
  22.     // }
  23.     maxLeft = Math.max(height[i], maxLeft);
  24.     maxRight = Math.max(height[len - i -1], maxRight);
  25.     s2 += maxRight;
  26.     s1 += maxLeft;
  27.     sum += height[i];
  28.   }
  29.   // 矩形面积
  30.   const recArea = maxLeft * len
  31.   // 积水面积 = S1 + S2 - 矩形面积 - 柱子面积
  32.   return s1 + s2 - recArea - sum;
  33. };