77. 组合

题目

题目来源：力扣（LeetCode）

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

思路分析

可以按照每一个数选与不选画出二叉树，二叉树最多 n 层。同样可以剪枝。剪枝的思路请见下图「剪枝条件 ② 的加强」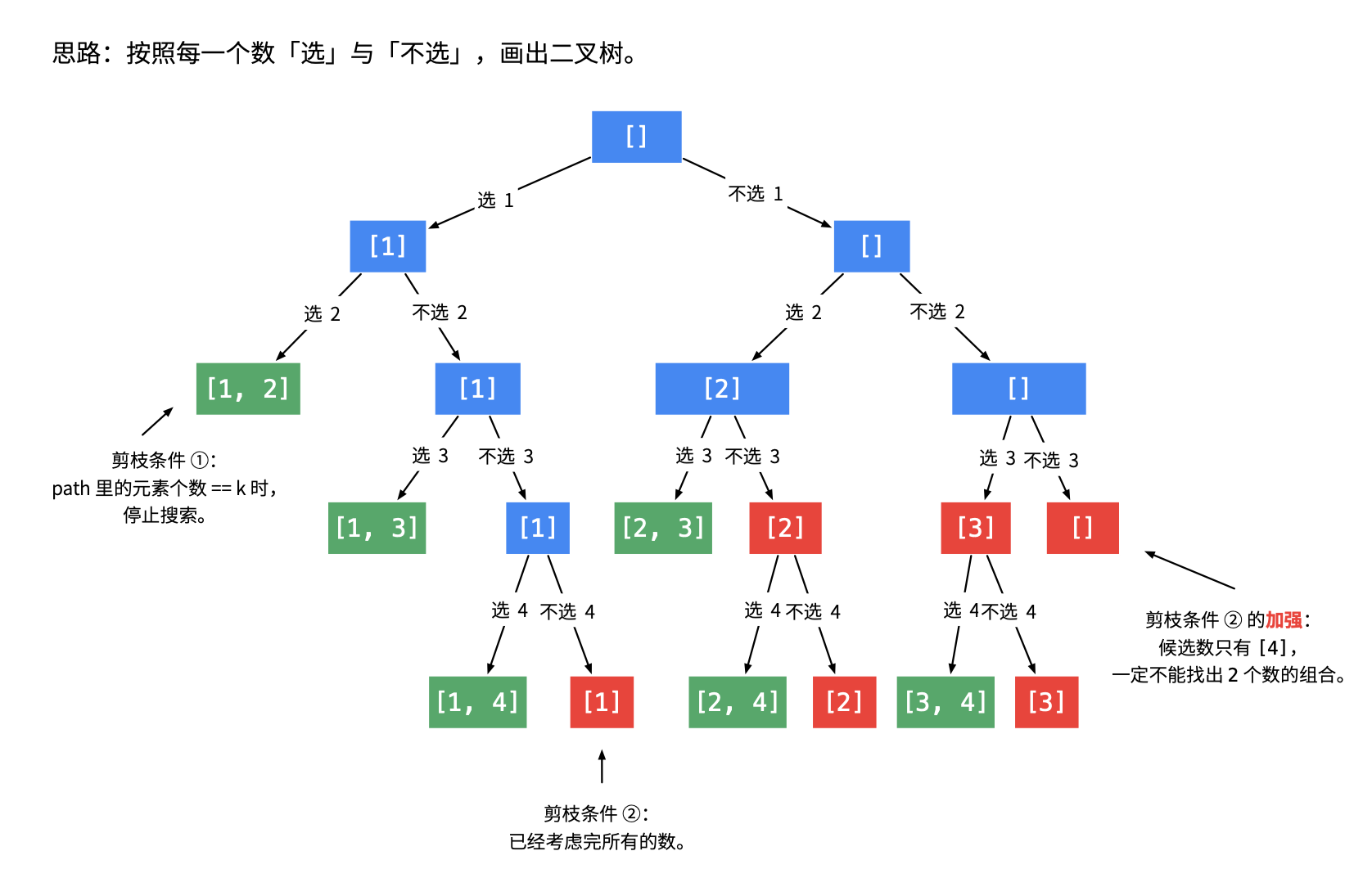

定义递归函数dfs(cur, n)， 参数表示当前位置是 cur，原序列总长度为 n。原序列的每个位置在答案序列种的状态有被选中和不被选中两种，我们用 temp 数组存放已经被选出的数字。在进入dfs(cur, n) 之前 [1, cur - 1] 位置的状态是确定的，而 [cur, n] 内位置的状态是不确定的，dfs(cur, n) 需要确定 cur 位置的状态，然后求解子问题dfs(cur + 1, n)。对于 cur 位置，我们需要考虑 a[cur] 取或者不取，如果取，我们需要把 a[cur] 放入一个临时的答案数组中（即上面代码中的 temp），再执行 dfs(cur + 1, n)，执行结束后需要对 temp 进行回溯；如果不取，则直接执行dfs(cur + 1, n)。在整个递归调用的过程中，cur 是从小到大递增的，当 cur 增加到 n + 1 的时候，记录答案并终止递归。

/**
 * @param {number} n
 * @param {number} k
 * @return {number[][]}
 */
var combine = function (n, k) {
  const ans = [];
  const dfs = (cur, n, k, temp) => {
    // 剪枝：temp 长度加上区间 [cur, n] 的长度小于 k，不可能构造出长度为 k 的 temp
    if (temp.length + (n - cur + 1) < k) {
      return;
    }
    // 记录合法的答案
    if (temp.length == k) {
      ans.push(temp);
      return;
    }
    // 考虑选择当前位置，递归到下一层
    dfs(cur + 1, n, k, [...temp, cur]);
    // 考虑不选择当前位置
    dfs(cur + 1, n, k, temp);
  }
  dfs(1, n, k, []);
  return ans;
};