题目

题目来源：力扣（LeetCode）

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

思路分析

动态规划

  1. 如果是台阶1，则只有一种爬法
  2. 如果是台阶2，则有两种爬法：
    • 先爬到台阶1，然后从台阶1爬到台阶2，
    • 直接调到台阶2
  3. 如果是台阶3，则有三种爬法：
    • 一阶一阶地往上爬
    • 直接跳到台阶2，然后爬上台阶3
    • 先爬上台阶1，然后直接调到台阶3

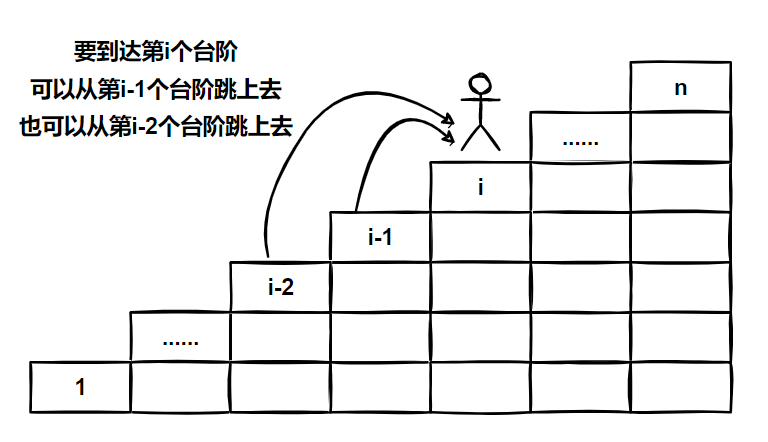
可以发现，爬到台阶3 的爬法就是爬到台阶2 的爬法 + 爬到台阶1 的爬法。

因此，我们定义 dp[i] 为爬到第 i 个台阶的方法数，
那么 dp[n] 为爬到第 n 个台阶的方法数，
由上面的分析，可得：
dp[1]=1
dp[2]=2

那么我们达到第 i 个台阶的方法数就等于到达第 i - 1 个台阶的方法数加上到达第 i - 2 个台阶的方法数，可得状态转移方程：dp[i] = dp[i -1 ] + dp[i - 2] 。

image.png
遍历实现：

  1. /**
  2.  * @param {number} n
  3.  * @return {number}
  4.  */
  5. var climbStairs = function (n) {
  6.   // 因为下面直接对dp[2]操作了，防止空指针
  7.   if (n <= 1) return n
  8.   // 为了与台阶数对应好理解，申请一个大小为 n+1 的数组 dp，
  9.   let dp = new Array(n + 1).fill(0);
  10.   // 初始状态
  11.   dp[1] = 1, dp[2] = 2;
  12.   // 注意i是从3开始的
  13.   for (let i = 3; i <= n; i++) {
  14.     dp[i] = dp[i - 1] + dp[i - 2];
  15.   } 
  16.   return dp[n];
  17. };

菲波那切数列数量求和

我们仔细观察状态转移方程 dp[i] = dp[i -1 ] + dp[i - 2] 与菲波那切数列数量求和公式 F(n)=F(n-1)+F(n-2)，两者是不是很相似呢？求有多少种不同的方法可以爬到楼顶，其实就是菲波那切数列数量求和。

递归实现：

  1. var climbStairs = function(n) {
  2.     const sqrt5 = Math.sqrt(5);
  3.     const fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);
  4.     return Math.round(fibn / sqrt5);
  5. };

参考阅读 https://leetcode-cn.com/problems/climbing-stairs/solution/70-pa-lou-ti-jie-shi-qing-chu-by-eill123-yxe1/ https://leetcode-cn.com/problems/climbing-stairs/solution/pa-lou-ti-cdong-tai-gui-hua-by-dululuya-1h4e/ https://leetcode-cn.com/problems/climbing-stairs/solution/yuan-lai-hui-pa-lou-ti-de-zheng-que-zi-s-pjez/