题目

题目来源：力扣（LeetCode

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。
返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出：[7,4,1]
解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1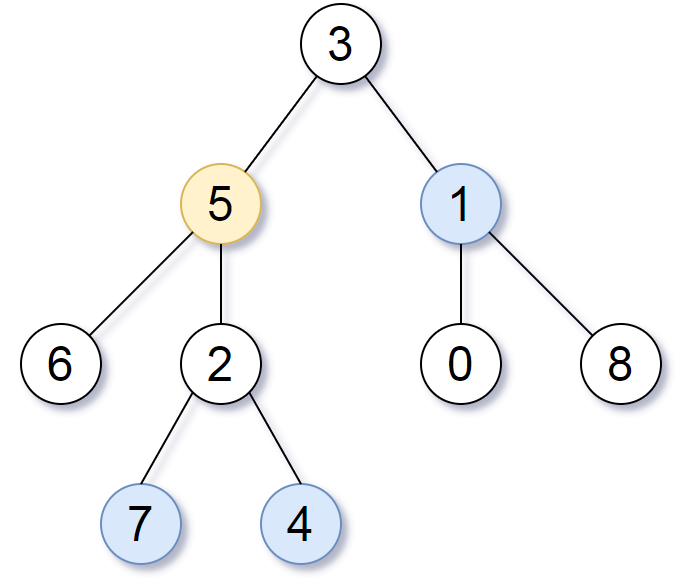
image.png

注意，输入的 “root” 和 “target” 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。

思路分析

解法一： 深度优先搜索 + 反向设置深度

  1. 找距离 target 为 k 的节点，其实就是找 以 target 为根节点，深度为 k 的节点；
  2. 首先使用深度优先搜索，找到目标节点 target，然后将 target 作为根节点，从 target 出发，使用深度优先搜索去寻找与 target 距离为 k 的所有节点，即深度为 k 的所有节点；
  3. 通常，node 每向上回溯一层，DFS 的限制深度就会减一，直至根节点，深度变为 0 （树从根结点开始往下数，叶子结点所在的最大层数称为 树的深度）；

  4. 我们反过来想，将 target 节点的深度置为 k，那么以 target 为根节点的树中，每向下一层，深度 减一，直至深度为 0 的节点，就是我们要找的节点。

    1. /**
    2. * Definition for a binary tree node.
    3. * function TreeNode(val) {
    4. *     this.val = val;
    5. *     this.left = this.right = null;
    6. * }
    7. */
    8. /**
    9. * @param {TreeNode} root
    10. * @param {TreeNode} target
    11. * @param {number} k
    12. * @return {number[]}
    13. */
    14. var distanceK = function(root, target, k) {
    15.  if (!root) return [];
    17.  let targetNode = null;
    18.  let res = [];
    19.  // 在递归过程中，存储已访问过的节点
    20.  let paths = [];
    21.  // 找到 target 节点，将其存储到 targetNode 中
    22.  findTarget(root, target);
    23.  // 以target 节点为根节点，向下寻找距离为 k 的节点
    24.  getDownDis(targetNode, k);
    25.  // 以 target 为根节点，向上寻找距离为 k 的节点
    26.  while(targetNode.parent && k > 0) {
    27.    targetNode = targetNode.parent;
    28.    getDownDis(targetNode, --k);
    29.  }
    31.  function findTarget(root, target) {
    32.    if (!root || targetNode) return;
    33.    // 找到 target 节点，存储到 targetNode 中
    34.    if (root.val === target.val) {
    35.      targetNode = root;
    36.    }
    37.    // 从左子树中找 target 节点
    38.    if (root.left) {
    39.      // 记录左孩子的父节点
    40.      root.left.parent = root;
    41.      findTarget(root.left, target);
    42.    }
    43.    // 从右子树中找 target 节点
    44.    if (root.right) {
    45.      // 记录右孩子的父节点
    46.      root.right.parent = root;
    47.      findTarget(root.right, target);
    48.    }
    49.  }
    51.  // node每向上回溯一层，DFS的限制深度就会减1，直到根节点root。若target在树中的深度为h, 且位于左子树中, 那么最后一次DFS就是在root与其右子树部分找出深度为k-h的所有节点
    52.  // 寻找离目标节点 target 的距离为 k 的节点：那么以 target 为根的树中，深度为 k 的所有节点显然符合要求
    53.  function getDownDis(node, k) {
    54.    // 已访问过的节点，不再访问
    55.    if (node === null || paths.indexOf(node) !== -1) return;
    56.    // 将未访问过的节点存储到 paths 中
    57.    paths.push(node);
    58.    if (k > 0) {
    59.      // 通常，node 每向上回溯一层，DFS 的限制深度就会减一，直至根节点，深度变为 0 （树从根结点开始往下数，叶子结点所在的最大层数称为 树的深度）
    60.      // 我们反过来想，将 target 节点的深度置为 k，那么以 target 为根节点的树中，每向下一层，深度 减一，直至深度为 0 的节点，就是我们要找的节点
    61.      getDownDis(node.left, k - 1);
    62.      getDownDis(node.right, k - 1);
    63.    } else if (k === 0) {
    64.      res.push(node.val);
    65.    }
    66.  }
    67.  return res;
    68. };

    辅助理解：https://leetcode-cn.com/problems/all-nodes-distance-k-in-binary-tree/solution/bfsyu-dfsde-tong-tai-yan-chu-by-my-xh-4gxn/

解法二：深度优先搜索 + 哈希表

  1. 我们将 target 作为根节点，从 target 出发，使用深度优先搜索寻找与 target 距离为 k 的所有节点，即深度为 k 的所有节点
  2. 由于输入的二叉树没有记录父节点，因此，我们从根节点 root 出发，使用深度优先搜索遍历整棵树，同时用一个哈希表记录每个节点的父节点
  3. 然后从 target 出发，使用深度优先搜索遍历整棵树，除了搜索左右子树外，还可以顺着父节点向上搜索
  4. 由于每个节点的值都是唯一的，因此哈希表的键可以用节点值代替。此外，为了避免在深度优先搜索时重复访问节点，递归是额外传入来源节点 from，在递归前比较目标节点是否与来源节点相同，不同的情况下才进行递归
  1. /**
  2.  * Definition for a binary tree node.
  3.  * function TreeNode(val) {
  4.  *     this.val = val;
  5.  *     this.left = this.right = null;
  6.  * }
  7.  */
  8. /**
  9.  * @param {TreeNode} root
  10.  * @param {TreeNode} target
  11.  * @param {number} k
  12.  * @return {number[]}
  13.  */
  14. var distanceK = function(root, target, k) {
  15.   const parents = new Map();
  16.   const ans = [];
  18.   const findParents = (node) => {
  19.     // DFS 左子树，记录每个节点的父节点
  20.     if (node.left != null) {
  21.       parents.set(node.left.val, node);
  22.       findParents(node.left);
  23.     }
  24.     // DFS 右子树，记录每个节点的父节点
  25.     if (node.right != null) {
  26.       parents.set(node.right.val, node);
  27.       findParents(node.right);
  28.     }
  29.   }
  31.   // 从 root 出发，深度优先搜索，记录每个节点的父节点
  32.   findParents(root);
  34.   const findAns = (node, from, depth, k) => {
  35.     if (node == null) return;
  36.     // 找到距离为 k 的节点
  37.     if (depth === k) {
  38.       ans.push(node.val);
  39.       return;
  40.     }
  41.     // 在左子树中寻找距离为k (即深度为k) 的节点
  42.     if (node.left !== from) {
  43.       findAns(node.left, node, depth + 1, k);
  44.     }
  45.     // 在右子树中寻找距离为k (即深度为k) 的节点
  46.     if (node.right !== from) {
  47.       findAns(node.right, node, depth + 1, k);
  48.     }
  49.     // 顺着父节点向上寻找距离为k (即深度为k) 的节点
  50.     if (parents.get(node.val) !== from) {
  51.       findAns(parents.get(node.val), node, depth + 1, k);
  52.     }
  53.   }
  55.   // 以 target 为根节点，从 target 出发，寻找所有深度为 k 的节点，根节点 target 的深度为 0 
  56.   findAns(target, null, 0, k);
  58.   return ans;
  59. };