搜索二维矩阵II

题目

题目来源：力扣（LeetCode

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：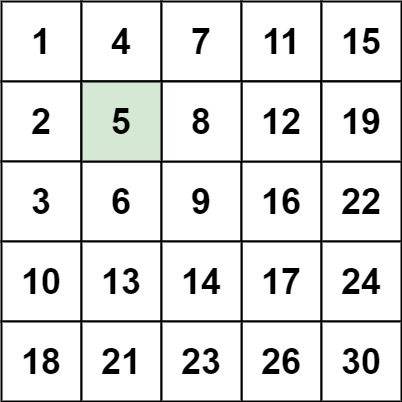

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：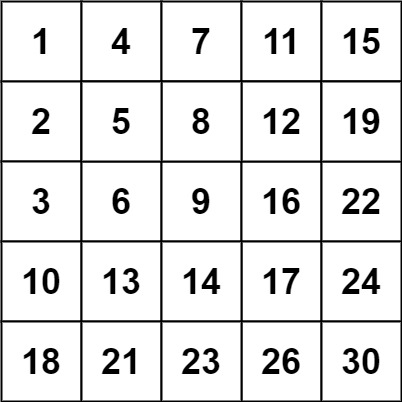

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

思路分析

数组从左到右和从上到下都是升序的，如果从右上角出发开始遍历呢？
会发现每次都是向左数字会变小，向下数字会变大，有点和二分查找树相似。二分查找树的话，是向左数字变小，向右数字变大。

所以我们可以把 target 和当前值比较。

如果 target 的值大于当前值，那么就向下走一行。
如果 target 的值小于当前值，那么就向左走一列。
如果相等的话，直接返回 true 。
也可以换个角度思考。

如果 target 的值小于当前值，也就意味着当前值所在的列肯定不会存在 target 了，可以把当前列去掉，从新的右上角的值开始遍历。

同理，如果 target 的值大于当前值，也就意味着当前值所在的行肯定不会存在 target 了，可以把当前行去掉，从新的右上角的值开始遍历。

我们来看最特殊的两个值，右上角15，左下角18。如果 target 大于15，因为第一行的最大值就是15，证明 target 一定不在第一行，所以我们当前位置往下移动一行找；如果 target 小于 15，15是最后一列的最小值，证明 target 不在最后一列 上，target 往左移动一列找。

var searchMatrix = function (matrix, target) {
    // 行
    let row = 0;
    // 列
    let col = matrix[0].length - 1;
    // 从右上角开始遍历
    while (row < matrix.length && col >= 0) {
        // row, col 等于待查找值
        if (matrix[row][col] == target) return true;
        // 从右上角开始遍历，如果当前值小于目标值，意味着当前值所在的行很定不会存在目标值了，向下移动一行，列不变，即 matrix[row][col] 变成 matrix[row + 1][col]，继续进行比较
        if (matrix[row][col] < target) row += 1;
        // 从右上角开始遍历，如果当前值大于目标值，意味着当前值所在的列很定不会存在目标值了，向下移动一列，行不变，即 matrix[row][col] 变成 matrix[row][col - 1]，继续进行比较
        else col -= 1;
    }
    return false;
};