两数之和 IV - 输入 BST

题目

题目来源：力扣（LeetCode）

给定一个二叉搜索树 root 和一个目标结果 k，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。

示例 1：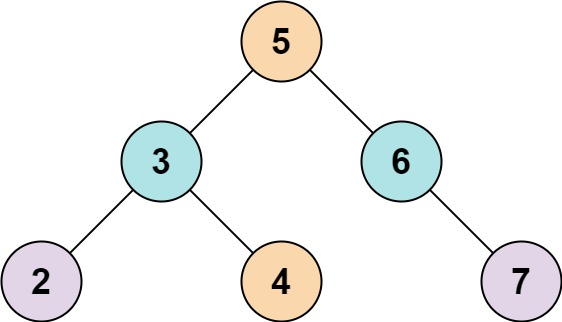

输入: root = [5,3,6,2,4,null,7], k = 9
输出: true

示例 2：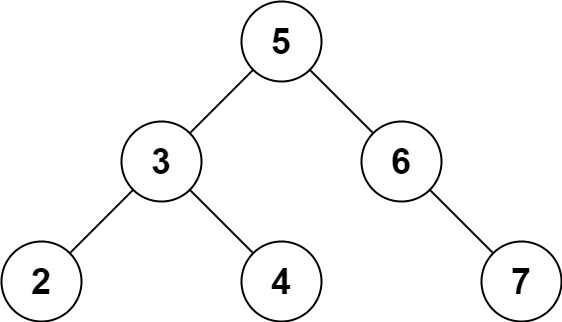

输入: root = [5,3,6,2,4,null,7], k = 28
输出: false

示例 3：

输入: root = [2,1,3], k = 4
输出: true

示例 4：

输入: root = [2,1,3], k = 1
输出: false

示例 5：

输入: root = [2,1,3], k = 3
输出: true

思路分析

中序遍历 + 双指针

二叉搜索树的中序遍历结果是一个升序序列，我们定义两个指针 left 和 right 分别指向升序序列的头部索引和尾部索引，然后执行以下操作：

1. 检查 left 和 right 索引处两元素之和是否等于 k。如果等于，则返回 True。

2. 如果当前两元素之和小于 k，则更新 left 指向下一个元素。这是因为当我们需要增大两数之和时，应该增大较小数。

3. 如果当前两元素之和大于 k，则更新 right 指向上一个元素。这是因为当我们需要减小两数之和时，应该减小较大数。

4. 重复步骤一至三，直到左指针 left 大于右指针 right。

5. 如果左指针 left到右指针 right 的右边，则返回 False。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {boolean}
 */
var inorder = function (root, ret) {
  if (root == null) return;
  inorder(root.left, ret);
  // ret数组中依次按着从小到大的顺序，存储二叉树的节点值
  ret.push(root.val);
  inorder(root.right, ret);
  return;
};
var findTarget = function (root, k) {
  let ret = [];
  // 中序遍历二叉搜索树
  inorder(root, ret);
  // 设置头指针left指向升序序列头部索引
  let left = 0;
// 设置尾指针 right 指向升序序列尾部索引
  let right = ret.length - 1;
  //
  while (left < right && ret[left] + ret[right] - k) {
    // left 和 right 索引处两元素之和如果小于k，头指针往后走，否则，尾指针往前走
    if (ret[left] + ret[right] < k) left += 1;
    else right -= 1;
  }
  // 如果left还是小于right,证明这个时候二叉排序树中存在两个值相加等于k
  return left < right;
};

广度优先搜索 + Set集合

我们定义一个 Set 集合存储遍历过的节点。使用广度优先搜索遍历二叉搜索树，首先将根节点加入 queue 中，然后执行以下步骤：

1. 从队列首部删除一个元素 p 。
2. 检查 setset 中是否存在 k - p。如果存在，返回 True。
3. 否则，将 pp 加入 set 。然后将当前节点的左孩子和右孩子加入 queue
4. 重复步骤一至三，直到 queue 为空。
5. 如果 queue 为空，返回 False。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {boolean}
 */
var findTarget = function (root, k) {
  const set = new Set();
  const queue = [];
  if (!root) return false
  queue.push(root)
  while (queue.length) {
    const node = queue.pop();
    if (set.has(k - node.val)) {
      return true
    }
    set.add(node.val)
    node.left != null && queue.push(node.left)
    node.right !=  null && queue.push(node.right)
  }
  return false
};