将二叉搜索树变平衡

题目

题目来源：力扣（LeetCode）

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

如果有多种构造方法，请你返回任意一种。

示例：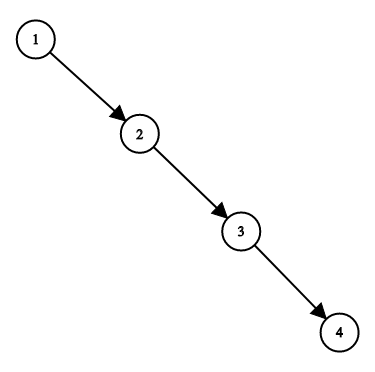

输入：root = [1,null,2,null,3,null,4,null,null]
输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

思路分析

AVL 树是一棵二叉搜索树，它具备自平衡的能力，它的左右子树都是 AVL 树，且左右子树的高度差的绝对值不超过1。

本题可用 AVL 树求解，但并不是最优解。

我们可以利用二叉搜索树的性质，中序遍历把二叉树转变为有序数组，然后取有序数组中间的元素作为根节点递归构造平衡二叉搜索树。

对于区间 [L, R]：

• 取 mid= ( L + R) / 2 ，即中心位置作为当前节点的值；
• 如果 L ≤ mid - 1，那么递归地将区间 [L, mid−1] 作为当前节点的左子树；
• 如果mid + 1 ≤ R，那么递归地将区间 [mid + 1, R] 作为当前节点的右子树。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var balanceBST = function (root) {
  // 存储中序遍历后得到的有序序列
  const trees = []
  // 中序遍历获取有序序列
  inorder(root)
  // 二分法递归构建平衡二叉搜索树
  return buildTree(trees)
  // 中序遍历构造有序序列
  function inorder(root) {
    if (root === null) return
    inorder(root.left)
    trees.push(root.val)
    inorder(root.right)
  }
  // 根据有序序列构建平衡二叉搜索树
  function buildTree(arr) {
    if (arr.length === 0) return null
    // 二分法获取中间节点作为平衡二叉搜索树的根节点
    const mid = arr.length >> 1
    const root = new TreeNode(arr[mid])
    // 递归构造左子树
    root.left = buildTree(arr.slice(0, mid))
    // 递归构造右子树
    root.right = buildTree(arr.slice(mid + 1))
    return root
  }
}